作业设计
教 材 上海九年义务教育课本 初一 第一学期 (试用本)
课 题 11.4中心对称
一.课堂训练
试 题 | 解 答 | 设计意图 |
A组: 1.在线段、射线、圆中,是中心对称图形的有______.它们的对称中心分别是 __________ .(补充) | 解:中心对称的图形有__________. 它们的对称中心是__________. | 补充了圆,学生已经学习过圆的有关常识,需要能理解和分辨中心对称图形和了解它的对称中心. |
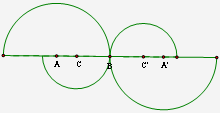
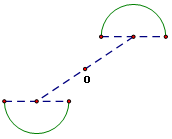
2.如图,请找出下列两图的对称中心.(补充)
|
| 分别联结两对应点,所得两条线段的交点就是对称中心.也可联结一组对应点,取线段的中点就是对称中心. |
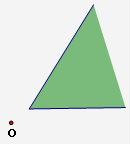
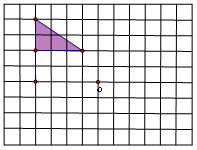
3.画出图中的三角形关于点O的中心对称的图形.
| 解:
所以此图即为所求图形. | 画出三角形关于某点的中心对称的图形,先确定三个顶点的对称点,再联结三个顶点即可. |
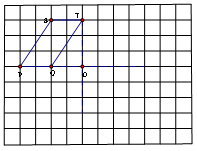
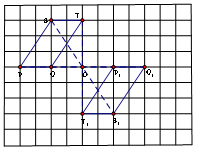
4.如图,有O、P、Q、S、T五点. (1)画出点P、Q、S、T关于点O的中心对称的点; (2)画出线段PS关于点O的中心对称的图形; (3)画出四边形PQTS关于点O的中心对称的图形. (课本P104/3);
| 解:
(1)点P1、Q1 、T1 、S1即为点P、Q、S、T关于点O的中心对称的点; (2)线段P1S1 即为线段PS关于点O的中心对称线段. (3)四边形P1Q1T1S1即为四边形PQTS关于点O的中心对称图形. | 在格点中正确画出四边形的各顶点的关于点O的对称点. |
5.画出如图所示的旗子关于点O的中心对称的图形.
(课本P104/3)
| 解:
所以此图即为所求图形. | 画不规则的中心对称的图形,重点在于找到每一个特殊点的对称点.领会日常图形的关于某点对称的图形.
|
B组: 如图,画出两个半圆关于点B成中心对称的图形.(补充)
| 解:
所以此图即为所求图形. | 训练册中有画不规则的中心对称的图形,所以补充了此题,它的重点在于找到每一个特殊点的对称点,所以先确定两个圆心的地方,画出它们关于点B的中心对称的点,依据两元半径画出图形即可. |
二.课后作业
试 题 | 解 答 | 设计意图 |
A组: ⒈下列图形中是中心对称图形的有 __________.(补充)
| 解:(2)(4).
| 正确区别中心对称图形与中心对称. |
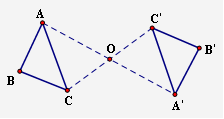
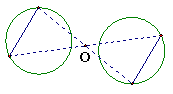
2.△ABC与△A′B′C′关于点O中心对称,请你描出对称中心O.(补充)
|
所以此图即为所求图形.
| 探寻对称中心,仅需分别联结两对对应点,所得两条直线的交点就是对称中心. |
3.画出图中四边形ABCD关于点O的中心对称的图形,并写出对应点.(训练册P64/1)
| 解:
所以四边形A′B′C′D′即为所求图形.A、B、C、D的对应点为A′、B′、C′、D′. | 能画出四边形ABCD关于点O的中心对称的图形. |
4.如图,画出三角形ABC关于点O的中心对称的图形 .(训练册P64/2)
|
所以△A1B1C1 即为所求图形.
| 在格点三角形中画出三角形的关于点O的中心对称的图形. |
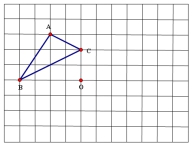
5.画出三角形ABC关于点O的中心对称的图形.(训练册P64/3)
|
所以△A′B′C′即为所求图形. | 能画出对称中心在形内的中心对称的图形. |
B组:画出半圆关于点O的中心对称的图形.(训练册P64/4尝试一下)
|
所以此图即为所求图形. | 先确定半圆的圆心,找到它的对称点,第二由半圆的半径长即可画出它的对称的图形.
|
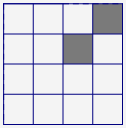
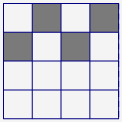
C组: 由16个相同的小正方形拼成的正方形网格.现将它中两个小正方形涂黑,请你在下图中再将它中两个小正方形涂黑,使它成为中心对称图形.(补充)
|
| 涂黑的两个小正方形的每个顶点都去尝试它的可能性,防止漏解,渗透分类讨论的数学思想. |





 解:
解: