华理科高2021学年第一学期期中考试
高二 数学学科 试题
满分分值：
150分 完卷时间：
120分钟
一．填空题（本大题共12题，第1-6题每小题4分，第7-12题每小题5分，满分54分）
1.已知平面内两点
，则向量
的单位向量的坐标为______________
2.
_____________
3.已知二元一次方程组
的增广矩阵为
，则方程组的解为_________
4.已知点
分线段
的比为-2，若
，则点的坐标为_______
5.三阶行列式
中元素-3的代数余子式的值为_________
6.已知等差数列
中，
，则
____________
7.设
，那样
_______________
8.已知，且
，则向量
与向量
的夹角为___________
9.已知数列的前
项和
，则
________
10.若正项数列是以
为公比的等比数列，已知该数列的每一项
的值都大于从开始的各项和，则公比的取值范围是______________
11.已知
的外接圆的圆心为
，半径为2，若
，且
，则向量
在向量
上的投影为___________
12.如图，等腰直角中，点为的重点，过点的直线与
两边分别交于
两点，且，则的最小值为________
二．选择题（本大题共有4题，满分20分）
13．给出下列命题：①在中，；②若A,B,C,D是不共线的四点，则是四边形
为平行四边形的充要条件；③若
且
，则；④若，且
。
其中正确的命题有（ ）
A.0个 B.1个 C.2个 D.3个
14.数列中，若
，
，则数列的极限为（ ）
A.0 B.0或 C. D.没有
15.已知
，假如在上的投影为
，则的值为（ ）
A.5 B.-5 C.
D.
16.数列中，满足
，
，设
，则（ ）
A.
B. C. D.
三．解答卷（本大题满分76分）本大题共有5题，解答下列各题需要写出必要的步骤。
17.（本题14分，每小题7分）
已知
，且与的夹角为
（1）求
；
（2）若，求实数
的值。
18.（本题14分，每小题7分）
已知O为坐标原点，
（1）若为锐角，求实数的取值范围；
（2）若是以
为直角的直角三角形，求实数的值并求的面积。
19.（本题14分，第（1）题6分，第（2）题8分）
数列中，，若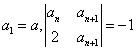
（1）求；
（2）猜想数列的通项公式，并用数学总结法证明。
20.（本题16分，第（1）小题4分，第（2），（3）小题各6分）
平面直角坐标系中，为坐标原点，射线与
轴正半轴重合，射线
在第一象限，且与轴正半轴的夹角为，在上有点列，在上有点
，已知
，
（1）求点和
的坐标；
（2）求
的坐标；
（3）求面积的最大值，并求出此时的值。
21.（本题18分，第（1）小题4分，第（2）小题6分，第（3）小题8分）
数列中，
，当
时，的前项和满足
（1）求的表达式；
（2）设，数列的前项和为，求；
（3）是不是存在正整数，使得成等比数列？若存在，求出
的值；若没有，请说明理由。
