2020中考数学压轴题全曝光精品专题02 一次方程的含参及应用问题

__________

               专题 02一次方程（组）的含参及应用问题

【考试知识点1】一次方程的有关概念

【例1】（2019•呼和浩特）关于x的方程mx2m﹣1+（m﹣1）x﹣2＝0若是一元一次方程，则其解为__________．

【答案】x＝2或x＝﹣2或x＝﹣3

【分析】∵关于x的方程mx2m﹣1+（m﹣1）x﹣2＝0若是一元一次方程，

∴当m＝1时，方程为x﹣2＝0，解得：x＝2；

当m＝0时，方程为﹣x﹣2＝0，解得：x＝﹣2；

当2m﹣1＝0，即m时，方程为x﹣2＝0，

解得：x＝﹣3，

故答案为：x＝2或x＝﹣2或x＝﹣3．

点睛：此题考查了一元一次方程的概念，熟练学会一元一次方程的概念是解本题的重点．

【变式1-1】（2019•湘西州）若关于x的方程3x﹣kx+2＝0的解为2，则k的值为__________．

【答案】4

【分析】∵关于x的方程3x﹣kx+2＝0的解为2，

∴3×2﹣2k+2＝0，

解得：k＝4．

故答案为：4．

点睛：此题主要考查了一元一次方程的解，正确把已知数据代入是解题重点．

【变式1-2】（2019•常州）若是关于x、y的二元一次方程ax+y＝3的解，则a＝__________．

【答案】1

【分析】把代入二元一次方程ax+y＝3中，

a+2＝3，解得a＝1．

故答案是：1．

点睛：本题运用了二元一次方程的解的要点，运算准确是解决此题的重点．

【考试知识点2】方程组的解法

【例2】（2019•南通）已知a，b满足方程组，则a+b的值为（）

A．2 B．4 C．﹣2 D．﹣4

【答案】A

【分析】，

①+②得：5a+5b＝10，

则a+b＝2，

故选：A．

点睛：此题考查知道二元一次方程组，借助了消元的思想，消元的办法有：代入消元法与加减消元法．

【变式2-1】（2019•荆门）已知实数x，y满足方程组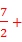则x2﹣2y2的值为（）

A．﹣1 B．1 C．3 D．﹣3

【答案】A

【分析】，

①+②×2，得5x＝5，解得x＝1，

把x＝1代入②得，1+y＝2，解得y＝1，

∴x2﹣2y2＝12﹣2×12＝1﹣2＝﹣1．

故选：A．

点睛：此题主要考查了二元一次方程组解的概念．与解二元一次方程组的基本办法．正确解关于x、y的方程组是重点．

【考试知识点3】方程组的含参问题

【例3】（2019•朝阳）关于x，y的二元一次方程组的解是，则m+n的值为（）

A．4 B．2 C．1 D．0

【答案】D

【分析】把代入得：，

解得：，

则m+n＝0，

故选：D．

点睛：此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．

【变式3-1】（2019•菏泽）已知是方程组的解，则a+b的值是（）

A．﹣1 B．1 C．﹣5 D．5

【答案】A

【分析】将代入，

可得：，

两式相加：a+b＝﹣1，

故选：A．

点睛：本题考查二元一次方程组的解，解题的重点是熟练运用二元一次方程组的解法，本题是基础题型．

【变式3-2】（2019•巴中）已知关于x、y的二元一次方程组的解是，则a+b的值是（）

A．1 B．2 C．﹣1 D．0

【答案】B

【分析】将代入得：

，

∴a+b＝2；

故选：B．

点睛：本题考查二元一次方程组的解；熟练学会方程组与方程组的解之间的关系是解题的重点．

【考试知识点4】二元一次方程的策略问题

【例4】（2019•天门）把一根9m长的钢管截成1m长和2m长两种规格均有些短钢管，且没余料，设某种截法中1m长的钢管有a根，则a的值可能有（）

A．3种 B．4种 C．5种 D．9种

【答案】B

【分析】设2m的钢管b根，依据题意得：

a+2b＝9，

∵a、b均为整数，

∴，，，．

故选：B．

点睛：本题运用了二元一次方程的整数解的要点，运算准确是解此题的重点．

【变式4-1】（2019•齐齐哈尔）学校计划购买A和B两种品牌的足球，已知一个A品牌足球60元，一个B品牌足球75元．学校筹备将1500元钱全部用于购买这两种足球（两种足球都买），该学校的购买策略共有（）

A．3种 B．4种 C．5种 D．6种

【答案】B

【分析】设购买A品牌足球x个，购买B品牌足球y个，

依题意，得：60x+75y＝1500，

∴y＝20x．

∵x，y均为正整数，

∴，，，，

∴该学校共有4种购买策略．

故选：B．

点睛：本题考查了二元一次方程的应用，找准等量关系，正确列出二元一次方程．

【考试知识点5】一次方程组的应用问题

【例5】（2019•娄底）某商场用14500元购进甲、乙两种矿泉水共500箱，矿泉水的本钱价与销价格如表（二）所示：

求：（1）购进甲、乙两种矿泉水各多少箱？

（2）该商场售完这500箱矿泉水，可获利多少元？

【答案】（1）购进甲矿泉水300箱，购进乙矿泉水200箱；

（2）该商场售完这500箱矿泉水，可获利5600元．

【分析】（1）设购进甲矿泉水x箱，购进乙矿泉水y箱，

依题意，得：，

解得：．

答：购进甲矿泉水300箱，购进乙矿泉水200箱．

（2）（35﹣25）×300+（48﹣35）×200＝5600（元）．

答：该商场售完这500箱矿泉水，可获利5600元．

点睛：本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的重点．

【变式5-1】（2019•百色）一艘轮船在相距90千米的甲、乙两地之间匀速航行，从甲地到乙地顺流航行用6小时，逆流航行比顺流航行多用4小时．

（1）求该轮船在静水中的速度和水流速度；

（2）若在甲、乙两地之间打造丙码头，使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同，问甲、丙两地相距多少干米？

【答案】（1）该轮船在静水中的速度是12千米/小时，水流速度是3千米/小时；

（2）甲、丙两地相距千米．

【分析】（1）设该轮船在静水中的速度是x千米/小时，水流速度是y千米/小时，

依题意，得：，

解得：．

答：该轮船在静水中的速度是12千米/小时，水流速度是3千米/小时．

（2）设甲、丙两地相距a千米，则乙、丙两地相距（90﹣a）千米，

依题意，得：，

解得：a．

答：甲、丙两地相距千米．

点睛：本题考查了二元一次方程组的应用与一元一次不等式的应用，解题的重点是：（1）找准等量关系，正确列出二元一次方程组；（2）找准等量关系，正确列出一元一次方程．

【变式5-2】（2019•呼和浩特）滴滴快车是一种便捷的出行工具，计价规则如下表：

小王与小张各自乘坐满滴快车，在同一地址约见，已知到达约见地址时他们的实质行车里程分别为6公里与8.5公里，两人付给滴滴快车的乘车费相同．

（1）求这两辆滴滴快车的实质行车时间相差多少分钟；

（2）实质乘车时间较少的人，因为出发时间比另一人早，所以提前到达约见地址在大厅等候．已知他等候另一人的时间是他一个人实质乘车时间的1.5倍，且比另一人的实质乘车时间的一半多8.5分钟，计算两个人各自的实质乘车时间．

【答案】（1）∴这两辆滴滴快车的实质行车时间相差19分钟；

（2）小王的实质行车时间为37分钟，小张的实质行车时间为18分钟．

【分析】（1）设小王的实质行车时间为x分钟，小张的实质行车时间为y分钟，由题意得：

1.8×6+0.3x＝1.8×8.5+0.3y+0.8×（8.5﹣7）

∴10.8+0.3x＝16.5+0.3y

0.3（x﹣y）＝5.7

∴x﹣y＝19

∴这两辆滴滴快车的实质行车时间相差19分钟．

（2）由（1）及题意得：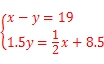

化简得

①+②得2y＝36

∴y＝18  ③

将③代入①得x＝37

∴小王的实质行车时间为37分钟，小张的实质行车时间为18分钟．

点睛：本题考查了二元一次方程和二元一次方程组在实质问题中的应用，依据等量关系列方程或方程组是解题的重点．

1．（2019•南充）关于x的一元一次方程2xa﹣2+m＝4的解为x＝1，则a+m的值为（）

A．9 B．8 C．5 D．4

【答案】C

【分析】由于关于x的一元一次方程2xa﹣2+m＝4的解为x＝1，

可得：a﹣2＝1，2+m＝4，

解得：a＝3，m＝2，

所以a+m＝3+2＝5，

故选：C．

点睛：此题考查一元一次方程的概念，重点是依据一元一次方程的定义和其解的定义解答．

2．（2019•阜新）某种衬衣因换季优惠供应，假如按原价的六折供应，那样每件赔本40元；按原价的九折供应，那样每件盈利20元，则这种衬衣的原价是（）

A．160元 B．180元 C．200元 D．220元

【答案】C

【分析】设这种衬衣的原价是x元，

依题意，得：0.6x+40＝0.9x﹣20，

解得：x＝200．

故选：C．

点睛：本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的重点．

3．（2019•鸡西）某学校计划用34件同样的奖品全部用于奖励在“经典诵读”活动中表现突出的班级，一等奖奖励6件，二等奖奖励4件，则分配1、二等奖个数的策略有（）

A．4种 B．3种 C．2种 D．1种

【答案】B

【分析】设一等奖个数x个，二等奖个数y个，

依据题意，得6x+4y＝34，

使方程成立的解有，，，

∴策略一共有3种；

故选：B．

点睛：本题考查二元一次方程的应用；熟练学会二元一次方程的解法是解题的重点．

4．（2019•孝感）已知二元一次方程组，则的值是（）

A．﹣5 B．5 C．﹣6 D．6

【答案】C

【分析】，

②﹣①×2得，2y＝7，解得，

把代入①得，x＝1，解得，

∴

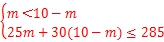
故选：C．

点睛：此题考查知道二元一次方程组，借助了消元的思想，消元的办法有：代入消元法与加减消元法．

5．（2019•乐山）《九章算术》第七卷“盈不足”中记载：“今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？”译为：“今有人合伙购物，每个人出8钱，会多3钱；每个人出7钱，又差4钱．问人数、物价各多少？”依据所学常识，计算出人数、物价分别是（）

A．1，11 B．7，53 C．7，61 D．6，50

【答案】B

【分析】设有x人，物价为y，可得：，

解得：，

故选：B．

点睛：本题考查了由实质问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的重点．

6．（2019•台州）一道来自课本的习题：

小红将这个实质问题转化为二元一次方程组问题，设未知数x，y，已经列出一个方程，则另一个方程正确的是（）

A． B． C． D．

【答案】B

【分析】设未知数x，y，已经列出一个方程，则另一个方程正确的是：．

故选：B．

点睛：此题主要考查了二元一次方程组的应用，正确理解题意得出等式是解题重点．

7．（2019•襄阳）《九章算术》是国内古时候数学名著，卷七“盈不足”中有题译文如下：今有人合伙买羊，每个人出5钱，会差45钱；每个人出7钱，会差3钱．问合作伙伴数、羊价各是多少？设合作伙伴数为x人，所列方程正确的是（）

A．5x﹣45＝7x﹣3 B．5x+45＝7x+3 C． D．

【答案】B

【分析】设合作伙伴数为x人，

依题意，得：5x+45＝7x+3．

故选：B．

点睛：本题考查了由实质问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的重点．

8.（2019•铁岭）若x，y满足方程组，则x+y＝__________．

【答案】7

【分析】，

①+②得：4x＝20，

解得：x＝5，

把x＝5代入②得：y＝2，

则x+y＝2+5＝7，

故答案为：7

点睛：此题考查知道二元一次方程组，熟练学会运算法则是解本题的重点．

9．（2019•咸宁）《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”译文大致是：“用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺？”假如设木条长x尺，绳子长y尺，可列方程组为__________．

【答案】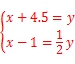

【分析】设木条长x尺，绳子长y尺，

依题意，得：．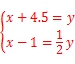

故答案为：．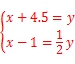

点睛：本题考查了由实质问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的重点．

10．（2019•眉山）已知关于x，y的方程组的解满足x+y＝5，则k的值为__________．

【答案】2

【分析】，

②×2﹣①，得3x＝9k+9，解得x＝3k+3，

把x＝3k+3代入①，得3k+3+2y＝k﹣1，解得y＝﹣k﹣2，

∵x+y＝5，

∴3k+3﹣k﹣2＝5，

解得k＝2．

故答案为：2

点睛：此题主要考查了二元一次方程组解的概念．与解二元一次方程组的基本办法．正确解关于x、y的方程组是重点．

11．（2019•自贡）某活动小组购买了4个篮球和5个足球，一共花费了466元，其中篮球的单价比足球的单价多4元，求篮球的单价和足球的单价．设篮球的单价为x元，足球的单价为y元，依题意，可列方程组为__________．

【答案】

【分析】设篮球的单价为x元，足球的单价为y元，由题意得：

，

故答案为：，

点睛：此题主要考查了由实质问题抽象出二元一次方程组，重点是正确理解题意，找出题目中的等量关系．

12．（2019•泰安）《九章算术》是国内古时候数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，买卖其一，金轻十三两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽视不计），问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，依据题意可列方程组为__________．

【答案】

【分析】设每枚黄金重x两，每枚白银重y两，由题意得：

，

故答案为：．

点睛：此题主要考查了由实质问题抽象出二元一次方程组，重点是正确理解题意，找出题目中的等量关系．

13．（2019•毕节市）某品牌旗舰店平时将某产品按进价提升40%后标价，在某次电子商务购物节中，为营销该产品，按标价8折销售，价格为2240元，则这种产品的进价是__________元．

【答案】2000

【分析】设这种产品的进价是x元，

由题意得，（1+40%）x×0.8＝2240．

解得：x＝2000，

故答案为2000

点睛：本题考查了一元一次方程的应用，解答本题的重点是了解题意，设出未知数，找出适合的等量关系，列方程解答．

14．（2019•南通）《九章算术》是中国传统数学非常重要的著作之一．书中记载：“今有人共买鸡，人出九，盈十一；人出六，不足十六．问人数几何？”意思是：“有若干人一同出钱买鸡，假如每个人出九钱，那样多了十一钱；假如每个人出六钱，那样少了十六钱．问：共有几个人？”设共有x个人一同出钱买鸡，依据题意，可列一元一次方程为__________．

【答案】9x﹣11＝6x+16

【分析】设有x个人一同买鸡，依据题意得：

9x﹣11＝6x+16．

故答案为：9x﹣11＝6x+16．

点睛：本题考查了由实质问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的重点．

15．（2019•烟台）亚洲文明对话大会召开期间，大量的大学生志愿者参与服务工作．某大学计划组织本校全体志愿者统一乘车去会场，若单独调配36座新能源客车若干辆，则有2人没座位；若只调配22座新能源客车，则用车数目将增加4辆，并空出2个座位．

（1）计划调配36座新能源客车多少辆？该大学共有多少名志愿者？

（2）若同时调配36座和22座两种车型，既保证每个人有座，又保证每车不空座，则两种车型各需多少辆？

【答案】（1）计划调配36座新能源客车6辆，该大学共有218名志愿者；

（2）需调配36座客车3辆，22座客车5辆．

【分析】（1）设计划调配36座新能源客车x辆，该大学共有y名志愿者，则需调配22座新能源客车（x+4）辆，

依题意，得：，

解得：．

答：计划调配36座新能源客车6辆，该大学共有218名志愿者．

（2）设需调配36座客车m辆，22座客车n辆，

依题意，得：36m+22n＝218，

∴n．

又∵m，n均为正整数，

∴．

答：需调配36座客车3辆，22座客车5辆．

点睛：本题考查了二元一次方程组的应用与二元一次方程的应用，解题的重点是：（1）找准等量关系，正确列出二元一次方程组；（2）找准等量关系，正确列出二元一次方程．

16．（2019•淮安）某公司用火车和汽车运输两批物资，具体运输状况如下表所示：

试问每节火车车皮和每辆汽车平均各装物资多少吨？

【答案】每节火车车皮装物资50吨，每辆汽车装物资6吨

【分析】设每节火车车皮装物资x吨，每辆汽车装物资y吨，

依据题意，得，

∴，

∴每节火车车皮装物资50吨，每辆汽车装物资6吨；

点睛：本题考查二元一次方程组的应用；可以依据题意列出准确的方程组，并用加减消元法解方程组是重点．

17．（2019•河池）在某体育用品商店，购买30根跳绳和60个毽子共用720元，购买10根跳绳和50个毽子共用360元．

（1）跳绳、毽子的单价各是多少元？

（2）该店在“五•四”年轻人节期间拓展优惠活动，所有产品按同样的折数优惠销售．节日期间购买100根跳绳和100个毽子仅需1800元，该店的产品按原价的几折销售？

【答案】（1）跳绳的单价为16元/条，毽子的单件为4元/个；

（2）该店的产品按原价的9折销售．

【分析】（1）设跳绳的单价为x元/条，毽子的单件为y元/个，可得：，

解得：，

答：跳绳的单价为16元/条，毽子的单件为4元/个；

（2）设该店的产品按原价的a折销售，可得：（100×16+100×4）1800，

解得：a＝9，

答：该店的产品按原价的9折销售．

点睛：本题主要考查二元一次方程组及一元一次方程的应用，理解题意找到相等关系是解题重点．

18．（2019•泸州）某出租汽车公司计划购买A型和B型两种节能汽车，若购买A型汽车4辆，B型汽车7辆，共需310万元；若购买A型汽车10辆，B型汽车15辆，共需700万元．

（1）A型和B型汽车每辆的价格分别是多少万元？

（2）该公司计划购买A型和B型两种汽车共10辆，成本低于285万元，且A型汽车的数目少于B型汽车的数目，请你给出成本最省的策略，并求出该策略所需成本．

【答案】（1）A型汽车每辆的进价为25万元，B型汽车每辆的进价为30万元；

（2）最省的策略是购买A型汽车4辆，购进B型汽车6辆，该策略所需成本为280万元．

【分析】（1）设A型汽车每辆的进价为x万元，B型汽车每辆的进价为y万元，

依题意，得：，

解得，

答：A型汽车每辆的进价为25万元，B型汽车每辆的进价为30万元；

（2）设购进A型汽车m辆，购进B型汽车（10﹣m）辆，依据题意得：

解得：3≤m＜5，

∵m是整数，

∴m＝3或4，

当m＝3时，该策略所用成本为：25×3+30×7＝285（万元）；

当m＝4时，该策略所用成本为：25×4+30×6＝280（万元）．

答：最省的策略是购买A型汽车4辆，购进B型汽车6辆，该策略所需成本为280万元．

点睛：本题考查一元一次不等式组的应用、二元一次方程组的应用，解答本题的重点是明确题意，列出相应的不等式组和方程组，借助方程和不等式的性质解答．