因动点产生的代数最值问题
1.如图，抛物线
的图象与
轴交于
两点（点
在点
的左侧），与
轴交于点
，点
为抛物线的顶点．
（1）直接写出
三点的坐标；
（2）点
为线段
上一点（点不与点重合），过点作轴的垂线，与直线
交于点
，与抛物线交于点
，过点作
交抛物线于点，过点作轴于点
，若点在点左侧，当矩形的周长最大时，求
的面积；
（3）在（2）的条件下，当矩形的周长最大时，连接
，过抛物线上一点
作轴的平行线，与直线交于点
（点在点的上方）．若
，求点的坐标．
分析：（1）
（2）
∴抛物线的对称轴为直线
设
，其中
关于直线对称，∴设的横坐标为
则
∴周长
∴当
时，取最大值
此时
设直线的分析式为
则
解得
∴直线的分析式为
将代入得
（3）由（2）知，当矩形的周长最大时，
此时点，与点重合，
过作轴于
，则
是等腰直角三角形，
设，则
，解得
当
时，
当时，
或
2.如图1，抛物线平移后过点和原点，顶点为，对称轴与轴相交于点，与原抛物线相交于点．
（1）求平移后抛物线的分析式并直接写出阴影部分的面积；
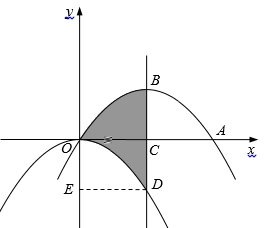
（2）如图2，直线与轴相交于点，点为线段
上一动点，
为直角，边与相交于点，设
，试探究：
①
为什么值时
为等腰三角形；
②为什么值时线段的长度最小，最小长度是多少．
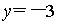
分析：（1）∵平移后的抛物线过原点
∴设平移后抛物线的分析式为
把代入，得
解得
∴平移后抛物线的分析式为
提示：
过作轴于
∵平移后的抛物线过点和原点
∴平移后的抛物线的对称轴为直线
把代入，得
（2）①
∴当时为等腰三角形
，
是的中点，
，，解得
∴当时为等腰三角形
②
连接
，作于
则
，即
在中，
当且仅当与重合，即时线段的长度最小，最小长度是
此时
