曹杨二中高中二年级期末数学试题
2020.01
1、 填空题
1. 三个平面最多把空间分成__________个部分
2. 若线性方程组的增广矩阵是
，解为
，则
__________
3. 若行列式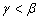
中元素
的代数余子式的值为5，则
__________
4. 已知圆锥的轴截面是等边三角形，侧面积为
，则圆锥的体积为__________
5. 已知四面体
的外接球球心在棱
上，且
，
，则外接球面上
两点、
间的球面距离是__________
6. 在正方体
中，二面角
的大小为__________
7. 若正四棱锥的地面边长为3，高为2，则这个正四棱锥的全方位积为__________
8. 已知是棱长为
的正四面体，则异面直线
与间的距离为__________
9. 若数列满足
，
，，则
__________
10. 某几何体的一条棱在主视图、左视图和俯瞰图中的长分别为1、2、3，则这条棱的长为
__________
11. 对于实数
，用
表示其小数部分，比如
，
，若
，
，则数列的各项和为__________
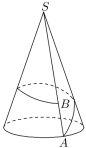
12. 如图是一座山的示意图，山呈圆锥形，圆锥的底面半径为
10公里，侧棱长为40公里，是
上一点，且公
里，为了进步旅游业，要建设一条最短的从绕山一周到
的观光铁路，这条铁路从出发后第一上坡，随后下坡，则
下坡段铁路的长度为__________公里
2、 选择题
13. 在学习等差数列时，大家由
，
，
，，得到等差
数列的通项公式是，像如此由特殊到普通的推理办法叫做（ ）
A. 不完全总结法 B. 完全总结法
C. 数学总结法 D. 剖析法
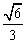14. 实行如图所示的程序框图，则输出的
的值为（ ）
A. B. 6 C. 14 D. 18
15. 已知三棱锥的底面是正三角形，且侧棱长均相等，
是棱上的点（不含端点），记直线与直线
所成角
为
，直线与平面所成角为
，二面角
的平面角为
，则（ ）
A. 
，
B. ，
C. ，
D. 
，
16. 已知平面与互相垂直，与交于，
和
分别是
平面、上的直线，若、均与既不平行，也不垂直，
则与的地方关系是（ ）
A. 可能垂直，但不可能平行 B. 可能平行，但不可能垂直
C. 可能垂直，也会平行 D. 既不可能垂直，也不可能平行
3、 解答卷
17. 如图，某公司制造一种海上用的“浮球”，它是由两个半球和一个圆柱筒组成，其中圆柱筒的高为2米，球的半径
为0.5米.
（1）求“浮球”的体积（结果精准到0.1立方米）；
（2）假设该“浮球”的建造成本仅与其表面积有关，已知圆柱形部分每平米建造成本为20元，半球形部分每平米建造成本为30元，求该“浮球”的建造成本.
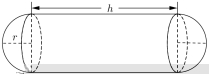（结果精准到1元）
18. 如图，在四棱锥
中，平面，且，
，，∥
，，.
（1）求异面直线与所成角的大小；
（2）求点到平面
的距离.
19. 已知数列的前项和为，且，.
（1）求证：数列
是等比数列；
（2）求当为什么值时，取最小值，并说明理由.
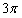20. 如图，在三棱柱中，
，
平面，
，
、分别是、的中点.
（1）求证：；
（2）求证：∥平面；
（3）求直线与平面所成角的正弦值的大小.
21. 对于给定的正整数（
），设集合，记集合.
（1）若
，求集合；
（2）若
是以
为首项，（）为公差的等差数列，求证：集合中的元素个数为；
（3）若是以
为首项，
为公比的等比数列，求集合中的元素个数及所有元素的和.
参考答案
1、 填空题
1. 8 2. 12 3. 4.
5. 6. 
7. 24 8. 
9. 
10. 11. 
12. 18
2、 选择题
13. A 14. B 15. B 16. D
3、 解答卷
17.（1）
；（2）220元.
18.（1）
；（2）.
19.（1）；（2）12.
20.（1）证明略；（2）证明略；（3）.
21.（1）
；（2）元数个数为个，和为
.
