勾股定理2及两点间距离公式（拓展）
（勾股定理，两点间距离公式）
本试题共有26道考试试题，满分100分，答卷时间90分钟
选择题（本大题共8道小题，每题3分，共24分）
1、如图是一株漂亮的勾股树，其中所有些四边形都是正方形，所有些三角形都是直角三角形．若正方A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是（ ）
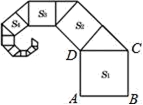
A. 13 B. 26 C. 34 D. 47
2、在直线l上有三个正方形m、q、n，若m、q的面积分别为5和11，则n的面积（ ）
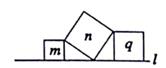
A. 4 
B. 6 C. 16 D. 55
3、如图，在矩形ABCD中，AB=6，BC=8，点E是BC边上一点，将△ABE沿AE折叠，使点B落在点F处，连结CF，当△CEF为直角三角形时，BE的长是（ ）
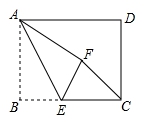
A. 4 B. 3 C. 4或8 D. 3或6
4、将矩形ABCD按如图方法折叠,点B,点C恰好落在点G处,且A,G,F在同一条直线上．若AB=4,BC=6,则CF的长是（ ）
A. 
B. 
C. 
D. 3
5、如图，矩形ABCD中，CD=6，E为BC边上一点，且EC=2将△DEC沿DE折叠，点C落在点C'.若折叠后点A，C'，E恰好在同一直线上，则AD的长为（ ）
A. 8 B. 9 C. 
D. 10
6、如图所示，将矩形ABCD纸对折，设折痕为MN，再把B点叠在折痕线MN上，（如图点B’），若 
，则折痕AE的长为（ ）
A. 
B. 
C. 2 D.
7、如图，将一个边长分别为8，16的矩形纸片ABCD沿EF折叠，使C点与A点重合，则EF与AF的比值为（ ）
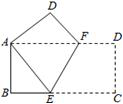
A. 4 
B. 
C. 2 D. 
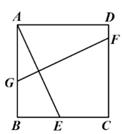
8、如图，在正方形ABCD中，点E是边BC上的一个动点，AE的垂直平分线分别交AB，CD于点G，F．若CF=6DF，则BE：EC的值为
A. 
B. 
C. 
D. 
2、填空题（本大题共12题，每题2分共24分）
9、在Rt△ABC中，∠ACB=90°，AD平分∠BAC与BC相交于点D，若BD=2，CD=1，则AC的长是________。
10、如图，在Rt△ABC中，∠B=90°，AB=30，BC=40，将△ABC折叠，使点B恰好落在边AC上，与点B重合，AE为折痕，则EB’=________．
11、如图，点D、E分别是直角△ABC的边AB和BC的点，将△BDE沿DE翻折到△ADE，若∠C=90°，AC=2 
，BC=8，则DE的长为________；
12、如图，在边长为1的正方形ABCD中，等边△AEF的顶点E、F分别在边BC和CD上则下列结论：①CE=CF：②∠AEB=75°；③S△EFC=1；④ ，其中正确的有________（用序号填写）
13、如图所示，有一块直角三角形纸片，∠C=90°，AC=8cm，BC=6cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则BD的长为________。
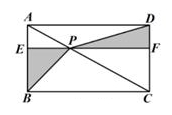
14、如图，在矩形ABCD中，点P在对角线AC上，过点P作EF∥BC，分别交AB，CD于点E，F，连结PB，PD．若PB= ，PD=6，图中阴影部分的面积为9，则矩形ABCD的周长为________．
15、如图，将一个长为9，宽为3的长方形纸片ABCD沿EF折叠，使点C与点A重合，则EF的长为________
16、如图，将直角三角形纸片AOB置于平面直角坐标系中，已知点A（0，3），B（4，0），将直角三角形纸片绕其右下角的顶点依次按顺时针方向旋转，首次旋转至图①地方，第二次旋转至图②地方，…，则直角三角形纸片旋转2019次后，其直角顶点与坐标轴原点的距离为________．
17、如图，正方形 
的边长为6，点 
是 
上的一点，连接 
并延长交射线 于点 
，将 
沿直线 翻折，点 
落在点 
处， 
的延长线交 于点 
，当 
时，则 
的长为____________.
18、如图，在平面直角坐标系中，O为坐标原点，四边形ABCD是平行四边形，点A、B、C的坐标分别为A（0，4），B（－2，0），C（8，0），点E是BC的中点，点P为线段AD上的动点，若△BEP是以BE为腰的等腰三角形，则点P的坐标为________．
19、在直线
上依次摆设着七个正方形（如图所示）. 已知斜放置的三个正方形的面积分别为1、2、3，正放置的四个正方形的面积依次是，则
__________.
20、如图，正方形ABCD的边长为2，其面积标记为S1 ， 以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2 ， ……根据此规律继续下去，则S2019的值为________.
3、简答卷（共7题，第21、22、23、24题每题8分，25、26每题10分，共52分）
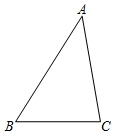
21、如图，△ABC的边AB=8，BC=5，AC=7．求BC边上的高．
22、如图所示，将一个长方形纸片ABCD沿对角线AC折叠.点B落在E点，AE交DC于F点，已知AB=8cm，BC=4cm.求折叠后重合部分的面积.
23、如图，P是长方形ABCD内一点，求证：
.
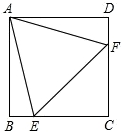
24、如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G，连接AG.
（1）求证：△ABG≌△AFG；
（2）求BG的长.
25、如图，在 中， 
是斜边 上两点，且 将 绕点 
顺时针旋转90°后，得到 连接
（1）求证： △AED≌△AEF
（2）猜想线段BE,ED,DC之间的关系，并证明
26、（1）如图①所示，P是等边△ABC内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转60°得△BCQ，连接PQ．若
，证明∠PQC=90°；
（2）如图②所示，P是等腰直角△ABC（∠ABC=90°）内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转90°得△BCQ，连接PQ．当PA、PB、PC满足哪些条件时，∠PQC=90°？请说明．
勾股定理2及两点间距离公式（拓展）
答案分析
1、单选题
1、D 2、C 3、D 4、A 5、D 6、C 7、B 8、C
2、填空题
9、 10、 11、 12、①②④ 13、
14、
15、 16、 17、 18、（1,4）或（6,4）或（0,4） 19、
20、 
3、解答卷
21、解：作AD⊥BC于D，
由勾股定理得，AD2=AB2-BD2 ， AD2=AC2-CD2 ，
∴AB2-BD2=AC2-CD2 ， 即82-（5-CD）2=72-CD2 ，
解得，CD=1，
则BC边上的高AD= ．
22、解：∵四边形ABCD是矩形，
∴∠D=∠B=90°，AD=BC=4cm，DC=AB=8cm，
∵ 将一个长方形纸片ABCD沿对角线AC折叠.点B落在E点，
∴EC=BC,∠B=∠E=90°，∴∠D=∠E=90°
又∠EFC=∠DFA，
∴△EFC≌△DFA，
∴DF=EF，AF=CF，
设FC=x，则DF=8-x，
在Rt△ADF中，DF2+AD2=AF2 ， 即（8-x）2+16=x2 ，
解得：x=5，即CF=5cm，
∴折叠后重合部分的面积= 
CF×AD=10cm2.
23、 易证，略
24、解：（1）∵四边形ABCD是正方形，
∴∠B=∠D=90°，AD=AB ，
由折叠的性质可知
AD=AF ， ∠AFE=∠D=90°，
∴∠AFG=90°，AB=AF ，
∴∠AFG=∠B ，
又AG=AG ，
∴△ABG≌△AFG；
（2）∵△ABG≌△AFG ，
∴BG=FG ，
设BG=FG= 
，则GC= ,
∵E为CD的中点，
∴CF=EF=DE=3，
∴EG= 
，
∴ 
，
解得 ，
∴BG=2
25、（1）证明：∵△ADC绕点A顺时针旋转90°得△AFB，
∴△ADC≌△AFB，∠FAD=90°，
∴AD=AF，
∵∠DAE=45°，
∴∠FAE=90°-∠DAE=45°，
∴∠DAE=∠FAE，
∵在△AED与△AEF中，
∴△AED≌△AEF（SAS）
（2）解：∵△AED≌△AEF，
∴ED=FE，∠ACB=∠ABF，
在Rt△ABC中，
∵∠ABC+∠ACB=90°，
∴∠ABC+∠ABF=90°即∠FBE=90°，
∴BE2+BF2=FE2 ， 即BE2+DC2=DE2
26、（1）证明：由旋转的性质知：BP=BQ、PA=QC，∠ABP=∠CBQ；
∵△ABC是等边三角形，
∴∠ABC=60°，即∠CBP+∠ABP=60°；
∵∠ABP=∠CBQ，
∴∠CBP+∠CBQ=60°，即∠PBQ=60°；
又∵BP=BQ，∴△BPQ是等边三角形；
∴BP=PQ；
∵PA2+PB2=PC2 ， 即PQ2+QC2=PC2；
∴△PQC是直角三角形，且∠PQC=90°
（2）解：PA2+2PB2=PC2；理由如下：
同（1）可得：△PBQ是等腰直角三角形，则PQ= PB，即PQ2=2PB2；
由旋转的性质知：PA=QC；
在△PQC中，若∠PQC=90°，则PQ2+QC2=PC2 ， 即PA2+2PB2=PC2；
故当PA2+2PB2=PC2时，∠PQC=90°
