《二次函数》测试题
一．选择题（每小题4分，共40分）
1、抛物线y=x2-2x+1的对称轴是
A、直线x=1B、直线x=-1C、直线x=2D、直线x=-2
2、下列命题：
①若
，则
；
②若
，则一元二次方程
有两个不相等的实数根；
③若
，则一元二次方程有两个不相等的实数根；
④若
，则二次函数的图像与坐标轴的公共点的个数是2或3.
其中正确的是（）．
Ａ.只有①②③ Ｂ．只有①③④ Ｃ．只有①④ Ｄ． 只有②③④．
3、对于
的图象下列叙述正确的是（）
A、顶点坐标为B、对称轴为y=3
C、当
时随
增大而增大D、当
时随增大而减小
4、如图，抛物线
的对称轴是直线
，且经过点（3，0），则
的值为
A. 0 B. －1 C. 1 D. 2
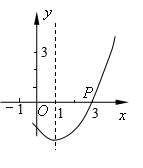
5、函数y=ax2的图象经过点，则a的值为（）
A.±2B.－2C.2D.3
6、自由落体公式h=gt2，h与t之间的关系是（）
A.正比率函数B.一次函数
C.二次函数D.以上答案都不对
7、下列结论正确的是（）
A.y=ax2是二次函数
B.二次函数自变量的取值范围是所有实数
C.二次方程是二次函数的特例
D.二次函数的取值范围是非零实数
8、下列函数关系中，可以看作二次函数
（
）模型的是（）
A、在一段距离内汽车的行驶速度与行驶时间的关系
B.国内人口年自然增长率为1%，如此国内人口总数随年份的变化关系
C.竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）
D.圆的周长与圆的半径之间的关系
9、对于任意实数m，下列函数肯定是二次函数的是（）
A．
B．
C．
D．
10、二次函数y=x2图象向右平移3个单位，得到新图象的函数表达式是（）
Ａ.y=x2+3Ｂ.y=x2-3
Ｃ.y=（x+3）2Ｄ.y=（x-3）2
第Ⅱ卷（非选择题，共80分）
2、填空题（每小题4分，共40分）
11、某工厂第一年的价值是20万元，第三年的价值是y万元，与平均年增长率x之间的函数关系式是＿＿＿＿＿＿＿＿。
12、已知二次函数的图像关于直线y=3对称，最大值是0，在y轴上的截距是－1，这个二次函数分析式为＿＿＿＿＿＿＿＿＿。
13、某学校去年对实验器材投资为2万元，预计今明两年的投资总额为y万元，年平均增长率为 x。则y与x的函数分析式＿＿＿＿＿＿。
14、m取＿＿＿时，函数
是以x为自变量的二次函数.
15、如图1所示，二次函数y=ax2+bx+c的图象开口向上，图象经过点（-1，2）和（1，0）且与y轴交于负半轴.
第（1）问：给出四个结论：①a>0；②b>0;③c>0；④a+b+c=0，其中正确的结论的序号是＿＿＿
第（2）问：给出四个结论：①abc<0；②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是＿＿＿＿.
16、杭州体博会期间，嘉年华游乐场投资150万元引进一项大型游乐设施，若不计修理保养成本，预计开放后每月可创收33万元，而该游乐设施开放后，从第1个月到第x个月的修理保养成本累计为y（单位：万元），且y=ax2+bx，若修理保养成本第1个月为2万元，第2个月为4万元；若将创收扣除投资和修理保养成本称为游乐场的纯收益g（单位：万元），g也是关于x的二次函数.
（1）y关于x的分析式＿＿＿＿＿＿＿＿＿；
（2）纯收益g关于x的分析式＿＿＿＿＿＿＿＿＿＿＿；
（3）设施开放＿＿＿＿个月后，游乐场纯收益达到最大？＿＿＿＿个月后，能收回投资？
17、已知：二次函数y=ax2+bx+c的图象如图所示，OA=OC，则由抛物线的特点写出如下含有a、b、c三个字母的等式或不等式：①
=-1；②ac+b+1=0；③abc>0；④a-b+c>0.
正确的序号是__________.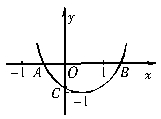 
18、已知抛物线y=ax2+bx+c（a>0）的对称轴为直线x=-1，与x轴的一个交点为（x1，0），且0
19、已知抛物线经过点（1，0），（-5，0），且顶点纵坐标为
，这个二次函数的分析式＿＿＿＿＿＿＿＿＿。
20、已知二次函数的图象开口向下，且经过原点.请写出一个符合条件的二次函数的分析式_____.
3、解答卷（共40分）
21、（8分）已知二次函数y=－x2+x+2 指出
函数图像的对称轴和顶点坐标；
把这个函数的图像向左、向下平移2个单位，得到哪一个函数的图像？
22、（6分）已知y是x的二次函数，当x=2时，y=－4，当y=4时，x恰为方程2x2－x－8=0的根，求这个函数的分析式。
23、（10分）某商场以每件42元的价钱购进一种服饰，依据试销得知：这种服饰天天的销量
（件），与每件的销价格
（元/件）可看成是一次函数关系：
（1）写出商场卖这种服饰天天的销售收益
与每件的销价格
之间的函数关系式（天天的销售收益是指所卖出服饰的销价格与购进价的差）；
（2）通过对所得函数关系式进行配方，指出：商场要想天天获得最大的销售收益，每件的销价格定为多少最为适合；最大销售收益为多少？
24、跳绳时，绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米，到地面的距离AO和BD均为0.9米，身高为1.4米的小丽站在距点O的水平距离为1米的点F处，绳子甩到最高处时刚好通过她的头顶点E.以点O为原点打造如图所示的平面直角坐标系, 设此抛物线的分析式为y=ax2＋bx＋0.9.
（1）求该抛物线的分析式；
（2）假如小华站在OD之间,且离点O的距离为3米，当绳子甩到最高处时刚好通过他的头顶，请你算出小华的身高；
（3）假如身高为1.4米的小丽站在OD之间,且离
点O的距离为t米, 绳子甩到最高处时超越她的头
顶,请结合图像,写出t的取值范围__________.
25（10分）．在某市拓展的环境创优活动中，某居民小区要在一块靠墙（墙长15米）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成，若设花园靠墙的一边长为x，花园的面积为y。
（1）求y与x之间的函数关系式，并写源于变量x的取值范围；
（2）满足条件的花园面积能达到200m2吗？若能，求出此时x的值，若不可以，说明理由：
（3）依据中求得的函数关系式，判断当x取何值时，花园的面积最大？最大面积是多少？
参考答案
1、1、A；提示：由于抛物线y=ax2+bx+c的对称轴方程是：y=-
，将已知抛物线中的a=1，b=-2代入，求得x=1，故选项A正确．
另一种办法：可将抛物线配方为y=a2+k的形式，对称轴为x=h，已知抛物线可配方为y=2，所以对称轴x=1，应选A．
2、B；
3、A、顶点坐标为
4、A
5、C.将（a,8）代入得a3＝8，解得a=2
6、C；是二次函数
7、B.二次函数自变量的取值范围是所有实数
8、C；竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）
9、C．对于任意实数m都是二次函数
10、D；本题考查的是抛物线的平移.先画出y=x2的草图，图象向右平移3个单位对称轴为x＝3，选项Ｄ中的二次函数的对称轴为x＝3.
2、11、函数关系式是
，即
12、由图像的对称轴和函数的最大值，可知顶点坐标是，设y=a2,
把x=0，y=－1代入，得9a=－1 ，a=－
，∴y=－2
13、设今年投资额为2（1+x）元，明年投资为2（1+x）2元
∴由题意可得.y=2+22=2x2+6x+4
14、若函数是二次函数，则
．解得 ，且
．
因此，当，且时，函数是二次函数．
15、解：（1）①，④；（2）②，③，④.
16、（1）y=x2+x；
（2）纯收益g=33x-150-（x2+x）
=-x2+32x-150
（3）g=-x2+32x-150=-（x-16）2+106，即设施开放16个月后游乐场的纯收益达到最大.
又在0
17、正确的序号为①②③④.
从图象中易知a>0，b<0，c<0，③正确；抛物线顶点纵坐标为-1，∴ ①对；当x=-1时y=a-b+c，由图象知（-1，a-b+c）在第二象限，∴ a-b+c>0，④正确；设C（0，c），则OC=|c|，∵ OA=OC=|c|，∴ A（c，0）代入抛物线得ac2+bc+c=0，又c≠0，∴ac+b+1=0，故②正确.
18、这是一道没给图象的题，由已知条件可以大致画出如下图所示的图象，∵ 0=-1， ∴ b=2a，∴ b-a=2a-a=a>0.∴ b>a>c，故②不正确；把b=2a代入a+b+c>0得3a+c>0， ∴ ③正确；故答案为2个.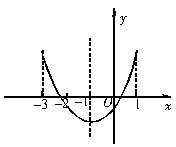
19、解：∵点（1，0），（-5，0）是抛物线与x的两交点,
∴ 抛物线对称轴为直线x=-2，
∴ 抛物线的顶点坐标为（－2，），
设抛物线的分析式为y＝ax2＋bx＋c，则有
∴ 所求二次函数分析式为
20、假如设二次函数的分析式为y=ax2+bx+c，由于图象开口向下，所以a为负数，图象过原点，即c＝0，满足这两个条件的分析式有无数个.
解：y＝－x2＋3x.
3、21、剖析:由以上探索求知，大伙已经了解函数y＝－2x2＋x－2的图象的开口方向、对称轴和顶点坐标.依据这类特征，可以使用描点法作图的办法作出函数y＝－2x2＋x－2的图象，进而察看得到这个函数的性质.
解：列表：在x的取值范围内列出函数对应值表；
x | … | －2 | －1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | －62 | －4 | －22 | －2 | －22 | －4 | －62 | … |
描点：用表格里各组对应值作为点的坐标，在平面直角坐标系中描点.
连线：用光滑的曲线顺次连接各点，得到函数y＝－2x2＋x－2的图象.
说明：列表时，应依据对称轴是x＝1，以1为中心，对称地选取自变量的值，求出相应的函数值。相应的函数值是相等的.
直角坐标系中x轴、y轴的长度单位可以任意定，且允许x轴、y轴选取的长度单位不同。所以要依据具体问题，选取适合的长度单位，使画出的图象美观.
则可得到这个函数的性质如下:
当x＜1时，函数值y随x的增大而增大；当x＞1时，函数值y随x的增大而减小；
当x＝1时，函数获得最大值，最大值y＝－2.
22、解：配方，y=－+2
=－2+3
∴图像的对称轴是直线x=2，顶点坐标为（2，3）。
把这个函数的图像向左、向下平移2个单位，顶点成为，形状不变，得到函数y=－x+1的图像。
23、解：本题不便求出方程2x2－x－8=0的根，设这个方程的根为x1、x2，则当
x=x1，x=x2时，y=4，可设y=a+4
把x=2，y=－4代入，得－4=a+4得a=4，所求函数为
y=4+4=8x2－4x－28
24、剖析：商场的价值是由每件产品的价值乘天天的销售的数目所决定。
在这个问题中，每件服饰的价值为（），而销售的件数是（
+204），那样就能得到一个与之间的函数关系，这个函数是二次函数.
需要销售的最大收益，就是需要这个二次函数的最大值.
解：（1）由题意，销售收益与每件的销价格之间的函数关系为
=（
－42）（－3＋204），即=－32+
8568
（2）配方，得=－3（－55）2+507
∴当每件的销价格为55元时，可获得最大收益，天天最大销售收益为507元.
25、解：（1）由题意得点E（1,1.4）, B, 代入y=ax2+bx+0.9得
解得
∴所求的抛物线的分析式是y=－0.1x2＋0.6x+0.9.
（2）把x=3代入y=－0.1x2＋0.6x+0.9得
y=－0.1×32＋0.6×3+0.9=1.8
∴小华的身高是1.8米
（3）1＜t＜5
