《4.5 角的比较与补（余）角》基础训练
1. 如图①，射线OC，OD分别在∠AOB的内部，外部，下列各式错误的是.
图①
A．∠AOB<∠AOD B．∠BOC<∠AOB
C．∠COD<∠AOD D．∠AOB<∠AOC
2. 在∠AOB的内部任取一点C，作射线OC，那样有.
A.∠AOC＝∠BOC B.∠AOC＞∠BOC
C.∠BOC＞∠AOB D.∠AOB＞∠AOC
3. 如图②，假如∠AOB＝∠COD，那样.
图②
A．∠1＞∠2 B．∠1＝∠2
C．∠1＜∠2 D．没办法确定
4. 点P在∠MAN的内部，现有4个等式：①∠PAM＝∠NAP；②∠PAN＝
∠MAN；③∠MAP＝∠MAN；④∠MAN＝2∠MAP，其中能表示AP是∠MAN的平分线的有.
A．1个 B．2个 C．3个 D．4个
5. 如图③，若有∠BAD＝∠CAD，∠BCE＝∠ACE，则下列结论中错误的是.
图③
A．AD是∠BAC的平分线
B．CE是∠ACD的平分线
C．∠BCE＝∠ACB
D．CE是∠ABC的平分线
6. 如图④，∠AOD－∠AOC＝.
图④
A．∠AOC B．∠BOC C．∠BOD D．∠COD
7. 下列说法正确的有.
①锐角的余角是锐角，锐角的补角是锐角；
②直角没补角；
③钝角没余角，钝角的补角是锐角；
④直角的补角还是直角；
⑤一个锐角的补角与它的余角的差为90°；
⑥两个角相等，则它们的补角也相等．
A．3个 B．4个 C．5个 D．6个
8. 若∠α＋∠β＝90°，∠β＋∠γ＝90°，则∠α与∠γ的关系是.
A．互余 B．互补
C．相等 D．∠α＝90°＋∠γ
9. 如图⑤，直线AB，CD交于点O，由于∠1＋∠3＝180°，∠2＋∠3＝180°，所以∠1＝∠2的依据是.
图⑤
A．同角的余角相等 B．等角的余角相等
C．同角的补角相等 D．等角的补角相等
10. 如图⑥，点O在直线AE上，OB平分∠AOC，∠BOD＝90°，则∠DOE和∠COB的关系是.
图⑥
A．互余 B．互补
C．相等 D．和是钝角
11. 若一个角为75°，则它的余角的度数为.
A．285° B．105° C．75° D．15°
12. 已知∠A＝70°，则∠A的补角为.
A．110° B．70° C．30° D．20°
13. 下列各图中，∠1与∠2互为余角的是.
14. 已知∠1和∠2互为余角，且∠2与∠3互补，则下列说法错误的是.
A．∠1＋∠2＝90° B．∠2＋∠3＝180°
C．∠3－∠1＝90° D．∠3－∠2＝90°－∠1
15. 如图⑦，直线AB与∠COD的两边OC，OD分别相交于点E，F，若∠1＋∠2＝180°.找出图中与∠2相等的角，并说明理由．
图⑦
答案和分析
【答案】
1. D 2. D 3. B 4. D 5. D
6. D 7. B 8. C 9. C 10. A
11. D 12. A 13. B 14. D
15. ∠3，∠4，∠6.
【分析】
1. 解：∠AOB与∠AOD的边OA重合，OB在∠AOD内，所以∠AOB<∠AOD，A正确；同理B、C正确；∠AOB和∠AOC的边AO重合，OC在∠AOB内，所以∠AOB>∠AOC，D错误．
故选D.
此题主要考查了角的大小比较，解题的重点是学会角的大小比较办法．
2. 解：在∠AOB的内部任取一点C，作射线OC，那样有∠AOB＞∠AOC.
故选D.
此题主要考查了角的大小比较，解题的重点是学会角的大小比较办法．
3. 解：由于∠AOB＝∠COD，所以∠1＋∠BOD＝∠2＋∠BOD，
所以∠1＝∠2.
故选B.
此题考查了角的和差，学会等量代换办法是解题的重点.
4. 解：由角的平分线的几何表示可知：①∠PAM＝∠NAP；②∠PAN＝∠MAN；③∠MAP＝∠MAN；④∠MAN＝2∠MAP，都能表示AP是∠MAN的平分线，共有4个.
故选D.
判断一条射线是否角的平分线，只须看这条射线是不是将角分成相等的两个角．
5. 解：由于∠BAD＝∠CAD，所以AD是∠BAC的平分线，A正确；
由于∠BCE＝∠ACE，所以CE是∠ACD的平分线，∠BCE＝∠ACB ，B、C正确，D错误.
故选D.
判断一条射线是否角的平分线，只须看这条射线是不是将角分成相等的两个角．
6. 解：由图可知，∠AOD－∠AOC＝∠COD，
故选D.
本题考查了角的和差，解题重点是学会角的和差计算办法.
7. 解：锐角的余角是锐角，锐角的补角是钝角，①错误；
直角有补角，直角的补角还是直角，②错误，④正确；
钝角没余角，钝角的补角是锐角，③正确；
若∠1是锐角，则它的补角为180°－∠1，它的余角为90°－∠1，那样这个锐角的补角与它的余角的差为－＝180°－∠1－90°＋∠1＝90°，⑤正确；
两个角相等，则它们的补角也相等，⑥正确，
故正确的有4个，
故选B.
主要紧扣锐角、直角、钝角、余角、补角的特点进行判断，除①②不正确外，其他说法都正确．
因为互余的两个角之和为90°，所以这两个角都为锐角；互补的两个角之和为180°，所以这两个角为一个锐角、一个钝角或两个角都为直角．
8. 解：由于∠α＋∠β＝90°，∠β＋∠γ＝90°，所以∠α、∠γ是∠β的补角，
依据同角的补角相等，∠α＝∠γ，
故选C.
此题考查的是补角的性质，依据“同角的补角相等”进行解答即可.
9. 解：由于∠1＋∠3＝180°，∠2＋∠3＝180°，所以∠1＝∠2的依据是同角的补角相等.
故选C.
此题考查的是补角的性质，依据“同角的补角相等”进行解答即可.
10. 解：由于∠BOD＝90°，所以∠COB＋∠COD＝90°，
又由于OB平分∠AOC，所以∠AOB＝∠COB，
所以∠DOE＝180°－∠AOB－∠BOD＝180°－∠COB－90°＝90°－∠COB，
所以∠DOE和∠COB的关系是互余.
故选A.
此题考查的是角平分线的性质和余角、补角的性质，可以依据图形正确找到角之间的和差关系，理解角平分线的性质和余角、补角的性质是解题的重点．
11. 解：若一个角为75°，则它的余角的度数为90°－75°＝15°，
故选D.
本题考查了余角的概念，假如两个角的和等于一个直角，就说这两个角互为余角，简称互余，其中一个角是另一个角的余角．
12. 解：已知∠A＝70°，则∠A的补角为180°－∠A＝180°－70°＝110°，
故选A.
本题考查了补角的概念，假如两个角的和等于一个平角，就说这两个角互为补角，简称互补，其中一个角是另一个角的补角.
13. 解：由于三角形的内角和为180°，所以选项B中，∠1＋∠2＝90°，
即∠1与∠2互为余角，
故选B.
此题考查的是余角的概念，学会三角形内角和定理和余角的概念是解题重点.
14. 解：由于∠1和∠2互为余角，所以∠1＋∠2＝90°，A正确；
由于∠2与∠3互补，所以∠2＋∠3＝180°，B正确；
∠3＝180°－∠2，∠1＝90°－∠2，
所以∠3－∠1＝－＝180°－∠2－90°＋∠2＝90°，C正确；
故选D.
此题考查的是余角、补角的概念，依据余角、补角的概念，正确找到角之间的和差关系是解题的重点．
15. 解：由图可知，∠1的补角有∠3、∠4，
由于∠1＋∠2＝180°，所以∠2是∠1的补角，
依据同角的补角相等，得∠2＝∠3＝∠4，
又由于∠2＋∠5＝180°，∠5＋∠6＝180°，所以∠2＝∠6，
所以图中与∠2相等的角有∠3，∠4，∠6.
已知∠1＋∠2＝180°，说明∠2是∠1的补角．依据同角的补角相等，找出图中∠1的其他补角和∠2的其他补角的补角，便可确定与∠2相等的角．
“同角的余角相等”“同角的补角相等”的实质是等量代换，在特定的背景下用起来更便捷．
《4.5 角的比较与补（余）角》提升训练
1. 如图①，将一副三角板折叠放在一块，使直角的顶点重合于点O，则∠AOC＋∠DOB＝．
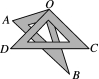
图①
A．120° B．180° C．150° D．135°
2. 如图②，点O在直线AB上，射线OC平分∠BOD，若∠COB＝35°，则∠AOD等于．
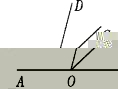
图②
A．35° B．70° C．110° D．145°
3. 借用一副三角尺，你能画出下面什么度数的角
A．65° B．75° C．85° D．95°
4. 如图③，OC平分平角∠AOB，∠AOD＝∠BOE＝20°，图中互余的角共有.
A．1对 B．2对 C．3对 D．4对
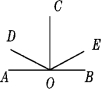
图③
5. 已知∠AOB＝70°，以O为端点作射线OC，使∠AOC＝42°，则∠BOC的度数为.
A．28° B．112° C．28°或112° D．68°
6. 如图④，直线AB与直线CD相交于点O，E是∠AOD内一点，已知OE⊥AB，∠BOD=45°，则∠COE的度数是.
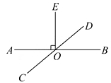
图④
A．125° B．135° C．145° D．155°
7. 如图⑤，已知直线AB，CD相交于点O，OE平分∠COB，若∠EOB＝55°，则∠BOD的度数是.
图⑤
A．35° B．55° C．70° D．110°
8. 如图⑥所示，已知AB为一条直线，O是AB上一点，OC平分∠AOD，OE在∠BOD内，∠DOE＝∠BOD，∠COE＝75°，求∠EOB的度数．
图⑥
9. 已知∠A与∠B互余，且∠A的度数比∠B度数的3倍还多30°，求∠B的度数．
10. 如图⑦，∠AOB＝120°，OD平分∠BOC，OE平分∠AOC.
求∠EOD的度数；
若∠BOC＝90°，求∠AOE的度数．
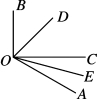
图⑦
答案和分析
【答案】
1. B 2. C 3. B 4. D 5. C 6. B 7. C
8. 9 ∠BCM或∠DCO
9. 15°
10. 60°；15°.
【分析】
1. 解：由图可得∠AOC＋∠DOB＝∠AOB＋∠COD＝90°＋90°＝180°.
故选B.
此题主要考查学生对角的计算的理解和学会，解答此题的重点是让学生通过察看图示，发现几个角之间的关系．
2. 解：由于射线OC平分∠BOD，∠COB＝35°，
所以∠BOD＝2∠COB＝70°，
所以∠AOD＝180°－∠BOD＝180°－70°＝110°，
故选C.
依据角平分线的性质可知，∠BOD＝2∠COB＝70°，由图可知，∠AOD与∠BOD互补，进而可以求出∠AOD的度数.
本题主要考查了角的断定，可以参考图形依次数出角的个数.
3. 解：一副三角尺的角有45°、45°、90°；30°、60°、90°.
故借用一副三角尺，可以画出45°＋30°＝75°的角.
故选B．
本题考查了三角尺有关的常识，学会三角尺的每个角的度数是解题重点.
4. 解：由于OC平分平角∠AOB，所以∠AOC＝∠BOC＝
∠AOB＝90°，
所以∠AOD与∠COD互余，∠BOE与∠COE互余，
又由于∠AOD＝∠BOE＝20°，所以∠BOE与∠COD互余，∠AOD与∠COE互余，
故图中互余的角共有4对.
故选D.
此题考查的是角平分线的性质和余角的性质，可以依据图形正确找到角之间的和差关系，理解角平分线的性质和余角的性质是解题的重点．
5. 解：如图⑧，当点C与点
重合时，∠BOC＝∠AOB－∠AOC＝70°－42°＝28°；
当点C与点重合时，∠BOC＝∠AOB＋∠AOC＝70°＋42°＝112°.
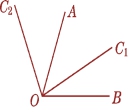
图⑧
故选C.
此题考查的是角的和差，本题要分两种状况进行讨论： 当点C与点重合时；当点C与点重合时，进而依据图形正确找到角之间的和差关系进行解答即可.
6. 解：由于OE⊥AB，所以∠AOE＝∠BOE＝90°，
又由于∠BOD＝45°，所以∠EOD＝∠BOE－∠BOD＝90°－45°＝45°，
所以∠COE＝180°－∠EOD＝180°－45°＝135°.
故选B.
此题考查的是余角、补角的概念，可以依据图形正确找到角之间的和差关系，理解余角、补角的概念是解题的重点．
7. 解：由于OE平分∠COB， 所以∠COE＝∠EOB，
由于∠EOB＝55°，所以∠COE＝55°，
所以∠BOD＝180°－∠COE－∠EOB＝180°－55°－55°＝70°.
故选C.
此题考查的是角平分线的性质和补角的概念，可以依据图形正确找到角之间的和差关系，理解角平分线的性质和补角的概念是解题的重点．
8. 解：设∠AOD的度数为x°，则∠BOD＝°.
由于OC平分∠AOD，∠DOE＝∠BOD，
所以∠COD＝∠AOD＝
，
∠DOE＝∠BOD＝°.
因为∠COE＝∠COD＋∠DOE＝75°，
因此，
＋＝75，解得x＝90.
所以∠BOD＝180°－∠AOD＝180°－90°＝90°，∠EOB＝
∠BOD＝60°.
几何题中包括多个已知量，条件包括多个数目关系，大家可选一个适合的量为x，再用这个x来表示其他未知量；借助方程思想进行计算，总是能达到意料之外的成效．
本题中用到角的平分线及角的和、差、倍、分关系，涉及的角较多，应注意借助这类数目关系将未知角用已知角表示出来．
9. 解：由于∠A与∠B互余，所以∠A＋∠B＝90°.
又由于∠A的度数比∠B度数的3倍还多30°，所以∠A＝3∠B＋30°，
所以3∠B＋30°＋∠B＝90°，
解得∠B＝15°.
故∠B的度数为15°.
依据∠A与∠B互余，得出∠A＋∠B＝90°，再由∠A的度数比∠B度数的3倍还多30°，从而得到∠A＝3∠B＋30°，再把两个算式联立即可求出∠B的值．
此题把角的关系结合方程问题一块解决，即把相等关系的问题转化为方程问题，借助方程组来解决．
10. 解：由于∠AOB＝120°，OD平分∠BOC，OE平分∠AOC，
所以∠EOD＝∠DOC＋∠EOC＝＝∠AOB＝×120°＝60°；
由于∠AOB＝120°，∠BOC＝90°，所以∠AOC＝120°－90°＝30°，
由于OE平分∠AOC，所以∠AOE＝∠AOC＝×30°＝15°.
依据OD平分∠BOC，OE平分∠AOC，可知∠DOE＝∠DOC＋∠EOC＝ ＝∠AOB，由此即可得出结论；先依据∠BOC＝90°求出∠AOC的度数，再依据角平分线的概念即可得出结论．
可以依据图形正确找到角之间的和差关系，理解角平分线的定义是解题的重点．
《4.5 角的比较与补（余）角》培优训练
1. 如图①，∠1＝∠2，∠3＝∠4，则下列结论：①AD平分∠BAF；②AF平分∠DAC；③AE平分∠DAF；④AF平分∠BAC；⑤AE平分∠BAC中，正确的有.
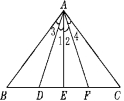
图①
A．4个 B．3个 C．2个 D．1个
2. 如图②，把一张长方形纸片沿EF折叠后，点D，C分别落在点D′，C′的地方，若∠DEF＝75°，则∠AED′等于.
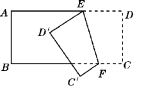
图②
A. 75° B. 65° C. 30° D. 25°
3. 假如∠α和∠β互补，且∠α＞∠β，则下列表示角的式子中：①90°－∠β；②∠α－90°；③；④．不可以表示∠β的余角的是.
A. ① B. ② C. ③ D. ④
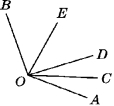
4. 如图③，OC是∠AOD的平分线，OE是∠BOD的平分线．
假如∠AOB＝130°，那样∠COE是多少度？
在的条件下，假如∠DOC＝20°，那样∠BOE是多少度？
图③
5. 如图④，已知∠AOB在∠AOC内部，∠BOC＝90°，OM，ON分别是∠AOB，∠AOC的平分线，∠AOB与∠COM互补，求∠BON的度数．
图④
答案和分析
【答案】
1. C 2. C 3. C
4. 65°；45°. 5. 15°
【分析】
1. 解：由于∠1＝∠2，所以AE平分∠DAF，③正确；
又由于∠3＝∠4，所以∠1＋∠3＝∠2＋∠4，即∠BAE＝∠CAE，所以AE平分∠BAC，⑤正确.
故正确的有2个.
故选C.
由角的平分线的几何表示可知：当∠1＝∠2时，AE平分∠DAF；再由∠3＝∠4可得∠1＋∠3＝∠2＋∠4，即∠BAE＝∠CAE，因此AE平分∠BAC.
判断一条射线是否角的平分线，只须看这条射线是不是将角分成相等的两个角．
2. 解：由折叠的性质可知，∠D′EF＝∠DEF，
由于∠DEF＝75°，所以∠D′EF＝75°，
所以∠AED′＝180°－∠D′EF－∠DEF＝180°－75°－75°＝30°.
故选C.
因为∠AED′＝180°－∠D′EF－∠DEF，∠DEF为已知角，而∠D′EF＝∠DEF，易求得∠AED′的度数．
折叠问题中的折痕平分被折边与原边的夹角．
3. 解：由概念知∠β的余角为90°－∠β，故①正确；
由于∠α和∠β互补，且∠α＞∠β，所以∠α＋∠β＝180°，∠α＞90°，所以∠β＝180°－∠α，所以∠β的余角为90°－＝∠α－90°，故②正确；
由于∠α＋∠β＝180°，所以＝90°，所以∠β的余角为90°－∠β＝－∠β＝，故④正确，而③错误．
故选C.
此题考查的是余角、补角的概念，可以正确找到角之间的和差关系，理解余角、补角的概念是解题的重点．
4. 解：由于OC平分∠AOD，所以∠DOC＝∠AOD.
由于OE平分∠BOD，所以∠DOE＝∠BOD.
所以∠COE＝∠DOC＋∠DOE＝ ＝∠AOB＝×130°＝65°.
由可知∠COE＝65°，由于∠DOC＝20°, 所以∠DOE＝∠COE－∠DOC＝45°.由于OE平分∠BOD，所以∠BOE＝∠DOE＝45°.
由已知可知∠DOC＝∠AOD，∠DOE＝∠BOD.因为∠COE＝∠DOC＋∠DOE，因此，∠COE＝∠AOD＋∠BOD＝∠AOB.
结合的结论可求出∠DOE的度数，从而求出∠BOE的度数．
借助角平分线进行计算时，要灵活运用角平分线的几种不同表达方法．在计算角的大小时，常常要用到等量代换，用已知角代替与它相等的未知角．
5. 解：由∠AOB与∠COM互补，得∠AOB＋∠COM＝180°.
由角的和差，得∠AOB＋∠BOM＋∠COB＝180°，∠AOB＋∠BOM＝90°.
由OM是∠AOB的平分线，得∠BOM＝∠AOB，即∠AOB＋∠AOB＝90°.
解得∠AOB＝60°.
由角的和差，得∠AOC＝∠BOC＋∠AOB＝90°＋60°＝150°.
由ON平分∠AOC，得∠AON＝∠AOC＝×150°＝75°.
由角的和差，得∠BON＝∠AON－∠AOB＝75°－60°＝15°.
依据补角的性质，可得∠AOB＋∠COM＝180°，依据角的和差，可得∠AOB＋∠BOM＝90°，依据角平分线的性质，可得∠BOM＝∠AOB，依据解方程，可得∠AOB的度数，依据角的和差，可得答案．
本题考查了余角与补角及角平分线的有关常识，借助了补角的性质，角的和差，角平分线的性质进行计算，解决问题必须要结合图形认真剖析，做到数形结合．
