2018-2019学年上海松江区初一（上）期末数学试题
1、选择题（本大题共6小题，共12.0分）
单项式-2x3y的系数与次数依次是（）
A. 
，3 B. ，4 C. 2，3 D. 2，4
下列各式运算正确的是（）
A. 
B. 
C. 
D. 
下列各等式中，从左到右的变形是因式分解的是（）
A. 
B. 
C. 
D. 
计算（-
）2018×（）2019的结果为（）
A. 
B. C. 
D. 
假如把分式中的都扩大2倍，那样分式的值（）
A. 扩大4倍 B. 扩大2倍 C. 缩小2倍 D. 不变
在正三角形、正方形、正五边形和等腰梯形这四种图形中，是旋转对称图形的有（）
 |
A. 1个 B. 2个 C. 3个 D. 4个
2、填空题（本大题共12小题，共24.0分）
用代数式表示：“x的2倍与y的差的平方”是______．
将0.000025用科学记数法表示为______．
将多项式xy3-x2y+2x3-5y2按字母x降幂排列是：______．
当x=3时，代数式
x2+2x-1的值为______．
当x______时，分式有意义．
因式分解：2x2-4x═______．
（x-3y）（x+3y）=______．
（2x-1）2=______．
计算：（4x2y-2xy2）÷2xy=______．
计算：
+
=______．
计算：（
）-1-（3.14-π）0=______．
如图，在长方形ABCD中，AB=7cm，BC=10cm，现将长方形ABCD向右平移3m，再向下平移4cm后到长方形A'B'C'D'的地方，A'B'交BC于点E，A'D'交DC于点F，那样长方形A'ECF的周长为______cm．
|
3、计算题（本大题共3小题，共15.0分）
计算：
-
计算：
÷（x+
）
解方程：-
=．
4、解答卷（本大题共9小题，共49.0分）
计算：3a2b•（-a4b2）+（a2b）3
计算：（a+b）（3a-2b）-b（a-b）．
计算：（m-n+1）（m+n+1）．
因式分解：（x-4）（x+7）+18．
因式分解：x2-4+4y2-4xy．
某校为了增强学生对中华出色传统文化的理解，决定购买一批有关的书本．据悉，经典著作的单价比传说的单价多6元，用10000元购买经典著作与用7000元购买传说的本数相同，这两类书本的单价各是多少元？
如图是由5个同样的小正方形所组成的，请再补上一个同样的小正方形，使6个小正方形组成的图形成为一个轴对称图形，请至少画出三种办法．
 |
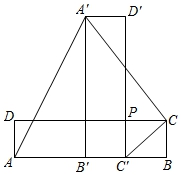如图，在长方形ABCD中，AB=a，BC=b（a＞2b），点P在边CD上，且PC=BC，长方形ABCD绕点P顺时针旋转90°后得到长方形A'B'C'D'（点B'、C'落在边AB上），请用a、b的代数式分别表示下列图形的面积．
（1）三角形PCC'的面积S1；
（2）四边形AA'CC'的面积S，并化简．
|
分式中，在分子、分母都是整式的状况下，假如分子的次数低于分母的次数，称如此的分式为真分式．比如，分式是
，
是真分式．假如分子的次数高于分母的次数，称如此的分式为假分式．比如，分式
，是假分式．一个假分式可以化为一个整式与一个真分式的和．比如，=
=1-．
（1）将假分式化为一个整式与一个真分式的和；
（2）假如分式的值为整数，求x的整数值．
答案和分析
1.【答案】B
【分析】
解：单项式-2x3y的系数与次数依次是：-2，4．
故选：B．
借助单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数，进而剖析即可．
此题主要考查了单项式，正确把握单项式的次数与系数确定办法是解题重点．
2.【答案】D
【分析】
解：A、3a-2a=a，故本选项不符合题意；
B、a6÷a3=a3，故本选项不符合题意；
C、（2a）3=8a3，故本选项不符合题意；
D、[（-a）2]3=a6，故本选项符合题意；
故选：D．
依据合并相同种类项法则、同底数幂的除法、幂的乘方和积的乘方分别求出每一式子的值，再得出选项即可．
本题考查了合并相同种类项法则、同底数幂的除法、幂的乘方和积的乘方等要点，能求出每一个式子的值是解此题的重点．
3.【答案】C
【分析】
解：A、x•（x-y）=x2-xy，不是因式分解，故本选项不符合题意；
B、x2+3x-1=x（x+3）-1，不是因式分解，故本选项不符合题意；
C、（x-y）2-y2=x（x-2y），是因式分解，故本选项符合题意；
D、x2-2=x（x-）式子右侧不是几个整式的积的形式，所以不是因式分解，故本选项不符合题意；
故选：C．
依据因式分解是把一个多项式化为几个整式的积的形式，进而判断即可．
本题考查了因式分解的概念，能熟记因式分解的概念的内容是解此题的重点，注意：把一个多项式化成几个整式的积的形式，叫因式分解．
4.【答案】A
【分析】
解：（-
）2018×（
）2019
=（-）2018×（）2018×
=．
故选：A．
直接借助积的乘方运算法则将原式变形得出答案．
此题主要考查了积的乘方运算，正确将原式变形是解题重点．
5.【答案】B
【分析】
解：把分式中的
都扩大2倍，
则=，
故分式的值扩大为原来的2倍．
故选：B．
直接借助分式的基本性质剖析得出答案．
此题主要考查了分式的基本性质，正确化简分式是解题重点．
6.【答案】C
【分析】
解：在正三角形、正方形、正五边形和等腰梯形，只有等边三角形、正方形、正五边形是旋转对称图形，共3个．
故选：C．
依据旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角，解答即可．
本题考查旋转对称图形的定义：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．
7.【答案】（2x-y）2
【分析】
解：由题意得：“x的2倍与y的差的平方”是（2x-y）2．
故答案为：（2x-y）2．
先求x的2倍，再求差，最后写出它们的平方即可求解．
本题考查了列代数式的常识，解答本题的重点是熟练读题，找出题目所给的等量关系．
8.【答案】2.5×10-5
【分析】
解：0.000025=2.5×10-5．
故答案为：2.5×10-5．
绝对值小于1的正数也可以借助科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不一样的是其所用的是负指数幂，指数由原数左侧起第一个不为零的数字前面的0的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左侧起第一个不为零的数字前面的0的个数所决定．
9.【答案】2x3-x2y+xy3-5y2
【分析】
解：将多项式xy3-x2y+2x3-5y2按字母x降幂排列是：2x3-x2y+xy3-5y2，
故答案为：2x3-x2y+xy3-5y2．
按x的指数从大到小排列各项即可．
本题考查多项式，考查的要点为：把一个多项式的各项根据某个字母的指数从大到小或从小到大的顺序排列，称为按这个字母的降幂或升幂排列．应该注意，在排列多项式各项时，要维持其原有些符号．
10.【答案】8
【分析】
解：当x=3时，
x2+2x-1=×32+2×3-1
=3+6-1
=8，
故答案为：8．
将x=3代入代数式，依据代数式需要的运算顺序列式计算可得．
此题考查了代数式求值，熟练学会运算法则是解本题的重点．
11.【答案】x≠-2
【分析】
解：依据题意得：x+2≠0，
解得：x≠-2．
故答案是：x≠-2．
依据分式有意义的条件是：分母不等于0，即可求解．
本题主要考查了分式有意义的条件，是一个基础题．
12.【答案】2x（x-2）
【分析】
解：2x2-4x=2x（x-2）．
故答案为：2x（x-2）．
直接提取公因式2x，进而分解因式即可．
此题主要考查了提取公因式法分解因式，正确找出公因式是解题重点．
13.【答案】x2-9y2
【分析】
解：（x-3y）（x+3y）=x2-9y2．
直接借助平方差公式，两个数的和乘以这两个数的差，等于这两个数的平方差计算即可．
本题主要考查平方差公式，熟记公式是解题的重点，计算时要找准这两个数．
14.【答案】4x2-4x+1
【分析】
解：原式=4x2-4x+1．
故答案为4x2-4x+1．
直接依据完全平方公式求解．
本题考查了完全平方公式：（a±b）2=a2±2ab+b2．也考查了代数式的变形能力．
15.【答案】2x-y
【分析】
解：（4x2y-2xy2）÷2xy=2x-y．
故答案为：2x-y．
直接借助整式的除法运算法则计算得出答案．
此题主要考查了整式的除法运算，正确学会运算法则是解题重点．
16.【答案】
【分析】
解：原式=
-=，
故答案为：．
先变形化为同分母分式相加减，再依据法则计算可得．
本题主要考分数查询式的加减法，解题的重点是熟练学会分式加减运算法则．
17.【答案】1
【分析】
解：（
）-1-（3.14-π）0
=2-1
=1．
故答案为：
1．
直接借助负指数幂的性质与零指数幂的性质分别化简得出答案．
此题主要考查了负指数幂的性质与零指数幂的性质，正确化简各数是解题重点．
18.【答案】20
【分析】
解：由题意得到BE=3cm，DF=4cm，
∵AB=DE=7cm，BC=10cm，
∴EC=10cm-3cm=7cm，FC=7cm-4cm=3cm，
∴长方形A'ECF的周长=2×（7+3）=20（cm），
故答案为20．
依据平移的距离表示出长方形A'ECF的长和宽，即可求出结论．
本题考查了平移的性质，认准图形，准确求出长方形A'ECF的长和宽是解题的重点．
19.【答案】解：原式=
-
=
=
．
【分析】
依据分式的减法法则计算可得．
本题主要考分数查询式的加减法，解题的重点是熟练学会分式的加减运算法则．
20.【答案】解：原式=
÷
=•=．
【分析】
原式括号中两项通分并借助同分母分式的加法法则计算，并借助除法法则变形，约分即可得到结果．
此题考查了分式的混合运算，熟练学会运算法则是解本题的重点．
21.【答案】解：方程两边都乘以6（x-1），得：3x-6=2（x-1），
解得x=4，
当x=4时，6（x-1）=18≠0，
所以原分式方程的解为x=4．
【分析】
第一去掉分母，然后解整式方程，最后验根即可求解．
本题考查知道分式方程的应用，解分式方程的重点是能把分式方程转化成整式方程．
22.【答案】解：原式=-2a6b3+a6b3
=-a6b3．
【分析】
先算乘方，再算乘法，最后合并即可．
本题考查了整式的混合运算，能熟练地运使用方法则进行计算是解此题的重点．
23.【答案】解：原式=3a2-2ab+3ab-2b2-ab+b2
=3a2-b2．
【分析】
先算乘法，再合并相同种类项即可．
本题考查了整式的混合运算，能熟练地运使用方法则进行计算是解此题的重点．
24.【答案】解：（m-n+1）（m+n+1）
=（m+1）2-n2
=m2+2m+1-n2．
【分析】
直接借助平方差公式将原式变形进而结合完全平方公式计算得出答案．
此题主要考查了平方差公式与完全平方公式，正确应用公式是解题重点．
25.【答案】解：（x-4）（x+7）+18
=x2+3x-10
=（x-2）（x+5）．
【分析】
直接借助多项式乘以多项式化简，再借助十字相乘法分解因式即可．
此题主要考查了十字相乘法分解因式，正确应用十字相乘法是解题重点．
26.【答案】解：x2-4+4y2-4xy
=x2+4y2-4xy-4
=（x-2y）2-4
=（x-2y+2）（x-2y-2）．
【分析】
直接将原式分组，再借助完全平方公式与平方差公式分解因式得出答案．
此题主要考查了分组分解法分解因式，正确运用公式是解题重点．
27.【答案】解：设传说的单价为x元/本，则经典著作的单价为（x+6）元/本，
依据题意得：
=，
解得：x=14，
经检验，x=14是所列分式方程的解，且符合题意，
∴x+6=20．
答：传说的单价为14元/本，经典著作的单价为20元/本．
【分析】
设传说的单价为x元/本，则经典著作的单价为（x+6）元/本，依据数目=总价÷单价结适用10000元购买经典著作与用7000元购买传说的本数相同，即可得出关于x的分式方程，解之经检验即可得出结论．
本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的重点．
28.【答案】解：如图所示：
．
【分析】
借助轴对称图形的性质得出符合题意的答案．
此题主要考查了借助轴对称设计图案，正确学会轴对称图形的性质是解题重点．
29.【答案】解：（1）由旋转可得，PC=PC'=b，∠单次点击成本'=90°，
∴△PCC'是等腰直角三角形，
∴△PCC'的面积S1=b2；
（2）由题可得，∠BCC'=45°，∠B=90°，A'B'=AB=a，
∴∠BCC'=∠BC'C=45°，
∴△BCC'是等腰直角三角形，
∴BC'=BC=b，BB'=2b，
∴AB'=a-b-b=a-2b，
∴四边形AA'CC'的面积S=S△AB'A'+S梯形A'B'BC-S△BCC'
=a（a-2b）+
-
=
-ab+ab+b2-
=+．
【分析】
（1）依据△PCC'是等腰直角三角形，即可得出△PCC'的面积S1=b2；
（2）依据△BCC'是等腰直角三角形，可得BC'=BC=b，BB'=2b，进而得到AB'=a-2b，再依据四边形AA'CC'的面积S=S△AB'A'+S梯形A'B'BC-S△BCC'进行计算即可．
此题考查了旋转的性质、矩形的性质的应用，解题时注意：对应点与旋转中心所连线段的夹角等于旋转角，旋转前、后的图形全等．
30.【答案】解：（1）由题可得，==2-
；
（2）=
=x+1+，
∵分式的值为整数，且x为整数，
∴x-1=±1，
∴x=2或0．
【分析】
（1）依据题意，把分式
化为整式与真分式的和的形式即可；
（2）依据题中所给出的例子，把原式化为整式与真分式的和形式，再依据分式的值为整数即可得出x的值．
本题考查了分式的混合运算，熟悉分式混合运算的法则是解答此题的重点．
