《1.5 有理数的乘除》基础训练
1. 三个数的乘积为0，则.
A. 三个数肯定都为0 B. 一个数为0，其他两个不为0
C. 三个数至少有一个是0 D. 两个数为0，另一个不为0
2. 若有理数a，b 满足ab>0，则必有.
A. a>0，b>0 B. a<0，b<0
C. a>0，b<0 D. a>0，b>0或a<0，b<0
3. 两个不为零的有理数相除，假如交换被除数与除数的地方，它们的商不变，那样这两个数.
A．肯定相等 B．肯定互为倒数
C．肯定互为相反数 D．相等或互为相反数
4. n个不等于0的有理数相乘，它们的积的符号.
A．由因数的个数决定 B．由正因数的个数决定
C．由负因数的个数决定 D．由负因数的大小决定
5. 下列各式积为正的是.
A．2×3×5× B．2×××
C．×0×× D．×××
6. 计算××0的结果是.
A．1.5 B．－1.5 C．0 D．1.2
7. 计算－5－×3的结果等于.
A．－11 B．－1 C．1 D．11
8. 计算12－7×＋8÷的结果是.
A．－24 B．－20 C．6 D．36
9. ×20××＝[×]×[20×]，运算中没运用的乘法运算律为.
A．交换律 B．结合律
C．分配律 D．交换律和结合律
10. 计算12＋÷－×2的结果是.
A．7 B．8 C．21 D．36
11. 在计算×时，可以防止通分的运算律是.
A．加法交换律 B．分配律
C．乘法交换律 D．加法结合律
12. 已知[－△]÷
＝0，那样△表示的数是.
A．－3 B．3 C．0 D．
13. 已知海拔高度每升高1000m，气温降低6℃.某人乘热气球旅游，在地面时测得温度是8℃，当热气球升空后，测得高空温度是－1℃，热气球的高度为________m.
14. 计算：
×－÷；
×.
15. 计算：
× ；
×
×
.
基础训练答案和分析
【答案】
1. C 2. D 3. D 4. C 5. D 6. C 7. C
8. D 9. C 10. C 11. B 12. A
13. 1500 14. －10
；39. 15. 11；
.
【分析】
1. 解：依据多个因数的乘法法则，三个数的乘积为0，则三个数至少有一个是0.
故选C.
由“几个数相乘，有一个因数为0，积就为0”可知，几个数的乘积为0，则至少有一个是0即可.
此题考查的是多个因数的乘法法则，几个数相乘，有一个因数为0，积就为0.
2. 解：由于ab>0，所以a，b异号，即a>0，b>0或a<0，b<0.
故选D.
两数相乘，积的符号是由两个乘数的符号决定：同号得正，异号得负. 已知ab>0，则a，b异号.
此题考查的是有理数的乘法法则，解题重点是理解“同号得正，异号得负”．
3. 解：两个不为零的有理数相除，假如交换被除数与除数的地方，它们的商不变，那样这两个数相等或互为相反数，
故选D.
依据有理数的除法法则：两数相除，同号得正，异号得负，并把绝对值相除解答．
此题考查的是有理数的除法法则，解题重点是理解“两数相除，同号得正，异号得负，并把绝对值相除”．
4. 解：n个不等于0的有理数相乘，它们的积的符号由负因数的个数决定.
故选C.
此题考查的是多个因数的乘法法则，几个不为0的数相乘，积的符号由负因数的个数决定.
本题的考试知识点是多个因数的乘法法则， 熟练学会多个因数的乘法法则是解题重点.
5. 解：×××，负因数有4个时，所以积为正.
故选D.
几个不为0的数相乘，积的符号由负因数的个数决定.当负因数有奇数个时，积为负；当负因数有偶数个时，积为正. 依据多个因数的乘法法则进行判断即可.
本题的考试知识点是多个因数的乘法法则， 熟练学会多个因数的乘法法则是解题重点.
6. 解：××0的因数中有0，故结果为0.
故选D.
几个数相乘，有一个因数为0，积为0. ××0的因数中有0，故结果为0.
此题考查的是多个因数的乘法法则，几个数相乘，有一个因数为0，积就为0.
7. 解：－5－×3＝－5－ ＝－5＋6＝1.
故选C.
根据先乘法，再减法的顺序进行计算即可.
此题考查的是有理数加减乘除混合运算的顺序，先算乘除，再算加减．
8. 解：
12－7×＋8÷＝12＋28－4＝36.
故选D.
根据先乘除，再加减的顺序进行计算即可.
此题考查的是有理数加减乘除混合运算的顺序，先算乘除，再算加减．
9. 解：察看式子可知，运算中运用了乘法交换律和结合律.
故选C.
由有理数的乘法运算律可知，×20××＝[×]×[20×]，运算中运用了乘法交换律和结合律.
此题考查的是有理数的乘法运算律，解题重点是熟练学会乘法运算律进行判断．
10. 解：
12＋÷－×2＝12＋3＋6＝21.
故选C.
根据先乘除，再加减的顺序进行计算即可.
此题考查的是有理数加减乘除混合运算的顺序，先算乘除，再算加减．
11. 解：察看式子可知，运算中运用分配律可以防止通分.
故选B.
由有理数的分配律可知，计算×时，运用分配律可以防止通分.
此题考查的是有理数的分配律，解题重点是熟练学会分配律进行判断．
12. 解：0除以一个不为0的数仍得0，故－△＝0，
所以，△＝－3，
故选A.
由“0除以一个不为0的数仍得0”可知，－△＝0，进而可以求出△的值.
此题考查的是有理数的除法法则，解题重点是理解“0除以一个不为0的数仍得0”.
13. 解：由题意可得，[8－]×＝1500，
故答案为1500.
解题时要正确理解题意，列出式子求解.
本题的考试知识点是有理数的混合运算的应用，结合题意，列出式子是解题的重点．
14. 解：×－÷
＝
×－
÷
＝－10－
＝－10－
＝－10
×
＝×
＝×
＝×－
×
＝36＋3
＝39
先计算括号内的，再按“先乘除，后加减”的顺序进行；
可考虑借助乘法的分配律进行方便计算．
在进行有理数的混合运算时，应先察看算式的特征，若能应用运算律进行简化运算，就先简化运算．
15. 解：×＝
×＋×＝20＋＝11；
××＝××＝
×＝
.
第题括号外面的因数－24是括号内每一个分数的倍数，相乘可以约去分母，使运算方便．借助乘法分配律进行方便运算．
第题－7可以与的分母约分，因此可借助乘法的交换律把它们先结合运算．
当一道题根据常规运算顺序去运算较复杂，而借助运算律改变运算顺序却可以使运算变得简 单些，这个时候可用运算律进行简化运算．
《1.5 有理数的乘除》提升训练
1. 假如两个有理数在数轴上的对应点在原点的同侧，那样这两个有理数的积.
A．肯定为正数 B．肯定为负数
C．为0 D．可能为正数，也会为负数
2. 若有2018个有理数相乘所得的积为零，则这2018个数中.
A．最多有一个数为0 B．至少有一个数为0
C．恰有一个数为0 D．均为0
3. 若两个非零有理数的和为零，则它们的商是.
A．－1 B．0 C．1 D．－1或1
4. 某冷藏库的室温为－5 ℃，有一批食品需要在－29 ℃的条件下冷藏．假如降温速度为
6 ℃/h，那样h后能降到所需的温度．
A．4 B. 3 C. 5 D. 2
5. 在如图所示的运算步骤中，若输入的数x＝3，则输出的数y＝．
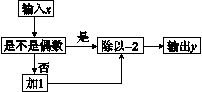
A．－2 B．
C．6 D．5
6. 假如a＋b＜0，
＞0，那样这两个数.
A．都是正数 B．符号没办法确定
C．一正一负 D．都是负数
7. 若一个有理数与－5互为倒数，则这个有理数的2倍与1的差为.
A．－11 B．9 C．
D．
8. 在数－5，1，－4，6，－3中任取两个数相乘，积的最小值为_______.
9. 概念新运算：a*b＝4a－3b－a×b，计算2*．
10. 一只小虫沿一根东西方向放置的木杆爬行，先以每分钟米的速度向西爬行了4分钟，后来又以同样的速度转身向东爬行了6分钟，求这个时候它与出发点的距离．
答案和分析
【答案】
1. A 2. B 3. A 4. A 5. A 6. D 7. C
8. －30 9. 23 10. 
米
【分析】
1. 解：假如两个有理数在数轴上的对应点在原点的同侧，则这两个有理数同号，那样这两个有理数的积肯定为正数.
故选A.
依据题意可得，两个有理数同号，“同号得正，异号得负”，则这两个有理数的积肯定为正数.
此题考查的是有理数的乘法法则，解题重点是理解“同号得正，异号得负”．
2. 解：依据多个因数的乘法法则，2018个有理数相乘所得的积为零，则这2018个数中至少有一个是0.
故选B.
由“几个数相乘，有一个因数为0，积就为0”可知，2018个数的乘积为0，则至少有一个是0即可.
此题考查的是多个因数的乘法法则，几个数相乘，有一个因数为0，积就为0.
3. 解：若两个非零有理数的和为零，则这两个有理数互为相反数，
依据有理数的除法法则可知，它们的商是－1.
故选A.
依据相反数的概念可知，这两个有理数符号不同，绝对值相等，则它们的商是－1.
此题考查的是有理数的除法法则，解题重点是剖析出“这两个有理数互为相反数”.
4. 解：依据题意可得，[ －]÷6＝24÷6＝4，
故4 h后能降到所需的温度．
故选A.
解题时要正确理解题意，列出式子求解.
本题的考试知识点是有理数的混合运算的应用，结合题意，列出式子是解题的重点．
5. 解：依据步骤图可列式为：y＝÷＝4÷＝－2，
故选A.
因为x＝3不是偶数，则y＝÷，求出y的值即可.
本题的考试知识点是有理数的混合运算的应用，结合步骤图，列出式子是解题的重点．
6. 解：由于＞0，依据“两数相除，同号得正”可知a、b同号，
又由于a＋b＜0 ，所以可以判断a、b均为负数．
故选D.
由有理数的除法法则可知，a、b同号，再依据有理数的加法法则，则可看出a、b均为负数．
此题考查了有理数除法和加法法则，解题时要灵活运使用方法则．
7. 解：依据倒数的概念可知，这个有理数为
，
则这个有理数的2倍与1的差为
.
故选C.
若两个有理数的乘积为1，大家称这两个有理数互为倒数. 则可以求出这个有理数，进而可以得到这个有理数的2倍与1的差.
此题考查的是有理数的混合运算和倒数的定义，解题重点是依据倒数的概念求出这个有理数，进而依据有理数混合运算法则进行计算即可.
8. 解：×1＝－5，×＝20，×6＝－30，×＝15，
1×＝－4，1×6＝6，1×＝－3，×6＝－24，×＝12，
6×＝－18，则积的最小值为－30.
故答案为－30.
依据题意，求出任意两个数的乘积，再比较大小即可.
此题考查的是有理数乘法法则，依据题意求出任意两个数的乘积是解题重点，进而比较乘积的大小即可．
9. 解：2*＝2×4－3×－2×＝8＋9＋6＝23.
依据新概念，列出算式求解即可.
此题考查的是有理数的混合运算法则，这种题的解题重点是要正确理解新概念．
10. 解：设向东方向为“＋”，则向西方向为“－”，依据题意可得，
×4＋×6＝×＝×2＝，
故小虫与出发点的距离为米.
第一要规定正方向，然后依据题意列出算式进行计算即可.
此题考查的是有理数混合运算的应用，解题重点是规定正方向，结合题意，列出算式.
《1.5 有理数的乘除》培优训练
1. 若x＋y＜0，xy＜0，x＞y，则有.
A．x＞0，y＜0，x的绝对值较大
B．x＞0，y＜0，y的绝对值较大
C．x＜0，y＞0，x的绝对值较大
D．x＜0，y＞0，y的绝对值较大
2. 如图①，在数轴上点A，B对应的有理数分别为a，b，则下列结论：①；②
；③
；④
.其中正确的有.
图①
A．1个 B．2个 C．3个 D．4个
3. 如图②是一个简单的数值运算程序，当输入的x的值为－1时，则输出的值为.
→→→
图②
A．1 B．－5 C．－1 D．5
4. 概念新运算：对于任意有理数a，b，都有a⊕b＝a＋1，等式右侧是一般的加法、
减法及乘法运算，譬如：2⊕5＝2×＋1＝2×＋1＝－6＋1＝－5.则3⊕的值是________.
5. 假如规定符号“*”的意义是a*b＝
－2a＋b，求[2*]*的值．
答案和分析
【答案】
1. B 2. B 3. C 4. 16 5.
【分析】
1. 解：∵xy＜0，
∴x、y异号，
又∵x＞y，
∴x＞0，y＜0，
∵x＋y＜0，
∴y的绝对值较大
故选B.
依据“两数相乘，同号得正，异号得负”可得x、y异号，再依据“异号两数相加，绝对值不相等时，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值”即可看出y的绝对值较大．
此题考查的是有理数加法法则和乘法法则， 熟练学会有理数加法法则和乘法法则是解题的重点.
2. 解：结合数轴可知，a＜0，b＞0，
两数相除，同号得正，异号得负，则
，，故①②错误；
依据相反数的概念可知，－a＞0，－b＜0，则，，故③④正确，
故正确的有2个，
故选B.
结合数轴可知，a＜0，b＞0，依据相反数的概念可知，－a＞0，－b＜0，进而对每一个选项进行判断即可.
此题主查考查有理数的除法法则，结合数轴和相反数的概念可判断a、b、－a、－b的符号，进而依据有理数的除法法则进行判断即可.
3. 解：当输入的x的值为－1时，则输出的值为×－3＝－1.
故选C.
依据给出的步骤图，列出算式，即可求出输出的值.
本题的考试知识点是有理数的混合运算的应用，结合步骤图，列出式子是解题的重点．
4. 解：3⊕＝3×[3－]＋1＝3×5＋1＝15＋1＝16.
依据新概念，列出算式求解即可.
此题考查的是有理数的混合运算法则，这种题的解题重点是要正确理解新概念．
5. 解：2*＝
＝6－4－3＝－1，
*＝
＝
＋2－1＝，
故[2*]*的值为.
依据给出的新概念，先求出2*的值，再求出[2*]*的值即可.
此题考查的是有理数的混合运算法则，这种题的解题重点是要正确理解新概念．
