第6课时平面向量的数目积
基础达标
1.若|a|=2,|b|=3,a,b的夹角θ为120°,则a·的值为.
A.12 B.-12 C.12
D.-12
【分析】由题意,得a·=4=4|a||b|cosplay θ=4×2×3×cosplay 120°=-12.
【答案】B
2.已知a=,b=,则a在b方向上的投影为.
A. B.
C.
D.
【分析】a在b方向上的投影为|a|cosplay θ=
=
=.
【答案】C
3.若平面向量a与b的夹角为60°,且a=,|b|=1,则|a+2b|等于.
A. B.2 C.4 D.12
【分析】由a=,则|a|=2,|a+2b|==
.
由于a·b=|a||b|cosplay 60°=2×1×
=1,
所以|a+2b|==
=2.
【答案】B
4.以A,B,C为顶点的三角形的形状是.
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
【分析】由已知得=,
=,∴·=-3×5+3×5=0,∴∠B=90°.
又||≠||,∴△ABC为直角三角形.故选B.
【答案】B
5.已知a⊥b,|a|=2,|b|=3,且3a+2b与λa-b垂直,则λ=__________.
【分析】∵⊥,∴·=0,
∴3λa2+a·b-2b2=0.
∵|a|=2,|b|=3,a⊥b,∴12λ-18=0,∴λ=
.
【答案】
6.若等边△ABC的边长为2
,平面内一点M满足
=
+
,则
·=__________.
【分析】如图所示,
·=·=
-
-
·
=
·
=
·
-
-
=
×2×cosplay 60°-×2-×2
=-2.
【答案】-2
7.已知三个点A,B,D.
求证:
⊥
;
要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD的两条对角线所成锐角的余弦值.
【分析】由于A,B,D,
所以=,
=.
又由于·=1×+1×3=0,所以⊥.
由于四边形ABCD为矩形,所以=
.
设点C的坐标为,则=.
所以
解得
所以点C的坐标为.
所以=.
又由于
=,
所以·=8+8=16,||=2
,||=2.
设与的夹角为θ,
则cosplay θ===
>0,
即与的夹角的余弦值为.
故矩形ABCD的两条对角线所成锐角的余弦值为.
拓展提高
8.已知O为坐标原点,点A,B的坐标分别为,,其中a∈,点P在AB上且=t,则
·的最大值为.
A.a B.2a C.3a D.a2
【分析】∵A,B,∴
=,=.
又∵=t,
∴
=+=+t=,
∴·=a=a2.
∵0≤t≤1,∴0≤1-t≤1,即·的最大值为a2.
【答案】D
9.设m,n是两个非零向量,且m=,n=,则下列等式中与m⊥n等价的个数为.
①m·n=0;②x1x2=-y1y2;③|m+n|=|m-n|;④|m+n|=.
A.1 B.2 C.3 D.4
【分析】由两个非零向量垂直的条件可知,①②正确.由模的计算公式与向量垂直的条件可知,③④也正确.
【答案】D
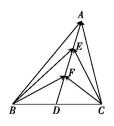
10.如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,·
=4,·
=-1,则
·
的值是__________.
【分析】·=·=·=
-
=2-=9
-=4,①
·
=·=·=-=-1,②
联立①②解得=
,=
.
∴·=·
=·
=
-=2-=4-
=4×-=.
【答案】
11.已知在△ABC中,非零向量与满足·
=0,且·=,试判断△ABC的形状.
【分析】由于表示与共线的单位向量,所以向量
+肯定与△ABC内角A的平分线共线,所以·=0说明△ABC中内角A的平分线与BC垂直,所以AB=AC.
由于·=,所以cosplay A=,所以A=
,
所以△ABC为等边三角形.
