上海交通大学附属中学度第一学期高中一年级数学期终试题
1、填空题（本大题共有12题，满分54分，1-6题每题4分，7-12题每题5分）
1. 若关于
的不等式
的解集为
，则实数
____________．
2. 设集合
，若
，则实数
的取值范围是____________．
3. 一条长度等于半径的弦所对的圆心角等于____________弧度．
4. 若函数
的反函数的图像经过点
，则实数____________．
5. 若
，则满足
的的取值范围是____________．
6. 已知是
上的增函数，那样的取值范围是____________．
7. 概念在
上的偶函数
，当时，
，则
在上的零点个数为____________．
8. 设
，
，则
的值为____________．
9. 设
为
的反函数，则
的最大值为____________．
10. 已知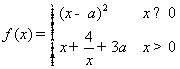
，若
是的最小值，则的取值范围是____________．
11. 设
，若函数
在区间
上有两个不一样的零点，则
的取值范围为____________．
12. 已知下列四个命题：
①函数
满足：对任意，有
；
②函数均为奇函数；
③若函数的图像关于点
成中心对称图形，且满足
，那样
；
④设
是关于的方程
的两根，则
其中正确命题的序号是____________．
2、选择题（本题共有4题，满分20分，每题5分
13. “”是“
”的（ ）
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分也非必要条件
14. 设函数
，则
的值为（ ）
A. B. 
C. 
中较小的数 D. 中较大的数
15. 下图中最大概是函数的图像是（ ）
A. 
B. 
C. D.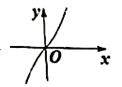
16. 若概念在上的函数满足：对任意有，则下列说法肯定正确的是（ ）
A. 为奇函数 B. 为偶函数
C. 为奇函数 D. 为偶函数
3、简答卷（第17题12分，第18-19题14分，第20-21题18分）
17. 解关于的不等式：
18. 设，函数；
（1）求的值，使得为奇函数；
（2）若
对任意的
成立，求的取值范围
19. 为了在夏天降温和冬天供暖时降低能源损耗，房子的屋顶和外墙需要建造隔热层。某幢建筑物要建造可用20年的隔热层，每厘米厚的隔热层建导致本为6万元。该建筑物每年的能源损耗成本（单位：万元）与隔热层厚度（单位：cm）满足关系，若不建隔热层，每年能源消耗成本为8万元。设为隔热层建造成本与20年的能源消耗成本之和。
（1）求
的值及的表达式；
（2）隔热层修建多厚时，总成本达到最小，并求最小值．
20.已知函数
.
（1）若
，求
在上的最小值；
（2）若
对于任意的实数恒成立，求的取值范围；
（3）当
时，求函数在上的最小值.
21. 对于概念在
上的函数，若函数满足：①在区间上单调递减；②存在常数
，使其值域为
，则称函数为函数的“线性替代函数”．
（1）求证：函数
不是函数
，的“逼近函数”；
（2）判断函数
是否函数
的“线性替代函数”；
（3）若是函数的“线性替代函数”，求的值
参考答案
1.4 2. 3. 4.3 5.
6.
7.0 8.7 9.4 10.
11. 12. ①②③④
13-16.BDAC
17、略
18、（1）；（2）
19、（1）
，
（2）当隔热层修建5cm时，总成本达到最小值70万元
20、（1）
；（2）；（3）1
21、（1）证明略；（2）是“线性替代函数”；（3）
